Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải:
Áp dụng định lý Py-ta-go vào tam giác HDF, ta có:
HF2 + DH2 = DF2
=> 162 + DH2 = 202
=> DH2 = 144 = 122
=> DH = 12 (cm)
Áp dụng định lý Py-ta-go vào tam giác DEH có:
DE2 = 92 + 122 = 225 = 152
=> DE = 15 (cm)
áp dụng định lý pitago vào tam giác DHF ta có:
HF2 + DH2 = DF2
hay 162+ DH2 = 202
suy ra : DH2= 144 =122
suy ra: DH = 12
áp dụng định lý pitago vào tam giác DEH ta có :
DE2 = 92+122= 225 = 152
suy ra : DE = 15

a . Áp dụng đl pytago đảo vào t/g DEF có :
DE^2 = EF^2 - DF^2 = 5^2 - 3^2 = 16
DE = 4
=> t/g DEF là tg vuông .
c . K ; H và M cùng nằm trên 1 đường thẳng không tạo t/g đc e nhé!

tu ve hinh :
cau b la vuong goc phai k
a, tamgiac ABC can tai A(gt) => AB = AC va goc ABC = goc ACB (dn)
goc ADB = goc ADC do AD | BC (GT)
=> tamgiac ADB = tamgiac ADC (ch - gn)
=> BD = DC (dn)
b, xet tamgiac BHD va tamgiac CKD co : BD = DC (Cau a)
goc ABC = goc ACB (cau a)
goc BHD = goc DKC = 90 do HD | AB va HK | AC (gt)
=> tamgiac BHD = tamgiac CKD (ch - gn)
=> HD = DK (dn)
c, xet tamgiac AHD va tamgiac AKD co : AD chung
HD = DK (cau b)
goc AHD = goc AKD = 90 do HD | AB va HK | AC (gt)
=> tamgiac AHD = tamgiac AKD (ch - cgv)
=> tamgiac AHK can tai A (dn)
=> goc AHK = (180 - goc BAC) : 2
tamgiac ABC can tai A (gt) => goc ABC = (180 - goc BAC) : 2
=> goc AHK = goc ABC 2 goc nay dong vi
=> HK // BC (tc)
d, tu ap dung py-ta-go

a: Xét ΔEHD và ΔEHF có
EH chung
\(\widehat{HED}=\widehat{HEF}\)
ED=EF
Do đó: ΔEHD=ΔEHF
c: Ta có; ΔEHD=ΔEHF
=>HF=HD
mà H nằm giữa D và F
nên H là trung điểm của DF
=>\(HD=\dfrac{DF}{2}=3\left(cm\right)\)
ΔEHD vuông tại H
=>\(EH^2+HD^2=ED^2\)
=>\(EH^2=5^2-3^2=16\)
=>\(EH=\sqrt{16}=4\left(cm\right)\)
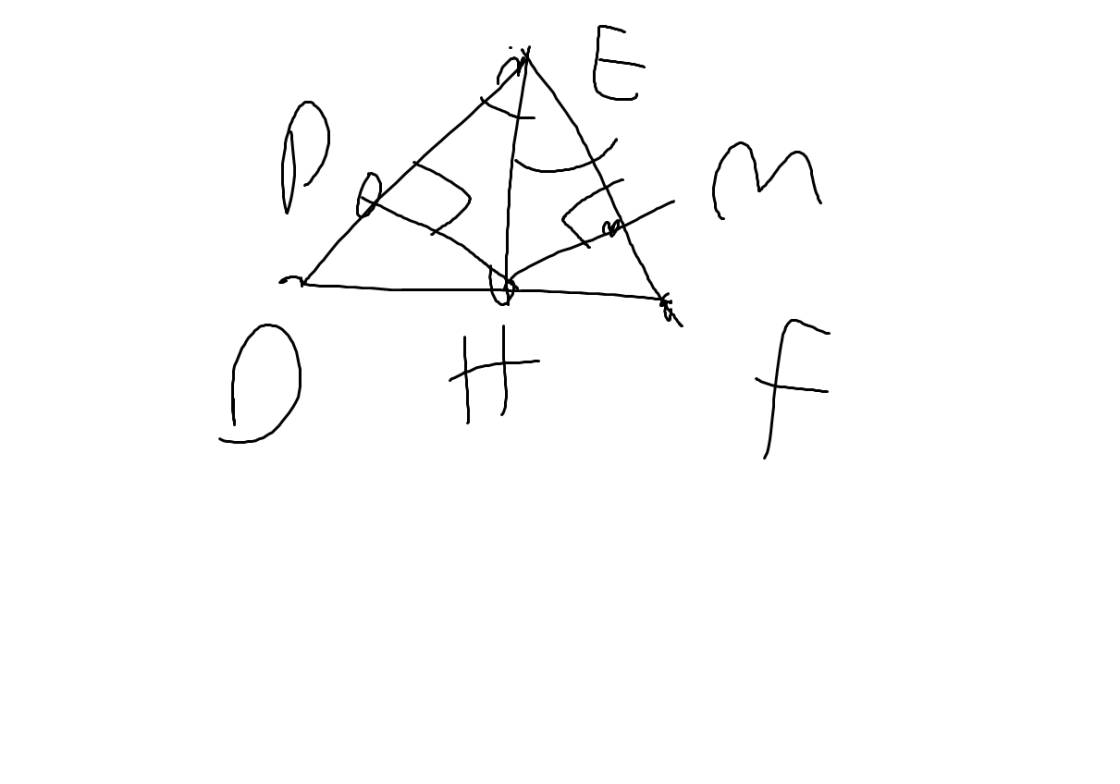

a: Xét ΔEHD và ΔEHF có
EH chung
\(\widehat{DEH}=\widehat{FEH}\)
ED=EF
Do đó: ΔEHD=ΔEHF
b: Xét ΔEPH vuông tại P và ΔEMH vuông tại M có
EH chung
\(\widehat{PEH}=\widehat{MEH}\)
Do đó: ΔEPH=ΔEMH
=>HP=HM
c: ΔDEF cân tại E
mà EH là đường phân giác
nên EH\(\perp\)DF và H là trung điểm của DF
H là trung điểm của DF
=>DH=HF=DF/2=6/2=3(cm)
ΔEHD vuông tại H
=>\(EH^2+HD^2=ED^2\)
=>\(EH^2+3^2=5^2\)
=>\(EH^2=5^2-3^2=25-9=16\)
=>\(EH=\sqrt{16}=4\left(cm\right)\)

a) Áp dụng định lí Pytago vào ΔDEF vuông tại D, ta được:
\(EF^2=DE^2+DF^2\)
\(\Leftrightarrow EF^2=9^2+12^2=225\)
hay EF=15(cm)
Vậy: EF=15cm
a, Theo định lí Pytago tam giác DHE vuông tại H
\(EH=\sqrt{DE^2-DH^2}=\dfrac{27}{5}cm\)
-> HF = 15 - 27/5 = 48/5 cm
Theo định lí Pytago tam giác DHF vuông tại H
\(DF=\sqrt{DH^2+HF^2}=12\)cm
b, Ta có \(EF^2=DE^2+DF^2\Rightarrow225=81+144\)(luôn đúng)
Vậy tam giác DEF vuông tại D
cảm ơn bạn nhìu❤