K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
22 tháng 10 2023
2:
a: Xét tứ giác OAMD có
\(\widehat{OAM}+\widehat{ODM}=90^0+90^0=180^0\)
=>OAMD là tứ giác nội tiếp
b: Xét (O) có
ΔADC nội tiếp
AC là đường kính
Do đó: ΔADC vuông tại D
=>AD\(\perp\)BC tại D
Xét ΔABC vuông tại A có AD là đường cao
nên \(AD^2=DB\cdot DC\)
Xét (O) có
MA,MD là tiếp tuyến
Do đó: MA=MD
=>\(\widehat{MAD}=\widehat{MDA}\)
mà \(\widehat{MAD}+\widehat{MBD}=90^0\)(ΔADB vuông tại D)
và \(\widehat{MDA}+\widehat{MDB}=\widehat{BDA}=90^0\)
nên \(\widehat{MDB}=\widehat{MBD}\)
=>MD=MB
mà MD=MA
nên MB=MA
=>M là trung điểm của AB
Xét ΔABC có
M,O lần lượt là trung điểm của AB,AC
=>MO là đường trung bình
=>MO//BC
12 tháng 9 2016
a + \(2\sqrt{a-\:1}\)= (a - 1) + \(2\sqrt{a-\:1}\)+ 1 = (\(1\:\:+\sqrt{a-1}\))2
Tương tự cho cái còn lại sẽ ra
6 tháng 11 2023
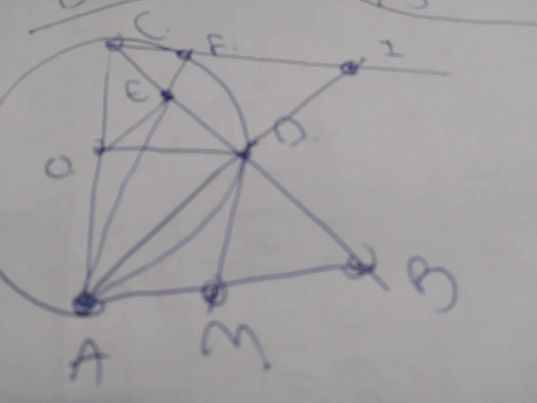
a: Kẻ OH vuông góc BC
=>OH là khoảng cách từ O đến BC
ΔOBC cân tại O
mà OH là đường cao
nên H là trung điểm của BC
=>\(HB=HC=\dfrac{BC}{2}=\dfrac{R\sqrt{3}}{2}\)
ΔOHB vuông tại H
=>\(OH^2+HB^2=OB^2\)
=>\(OH^2=OB^2-HB^2=R^2-\left(\dfrac{R\sqrt{3}}{2}\right)^2=\dfrac{R^2}{4}\)
=>OH=R/2
=>d(O;BC)=R/2
b: Xét ΔOBC có \(cosBOC=\dfrac{OB^2+OC^2-BC^2}{2\cdot OB\cdot OC}\)
=>\(cosBOC=\dfrac{R^2+R^2-3R^2}{2\cdot R\cdot R}=\dfrac{-1}{2}\)
=>\(\widehat{BOC}=120^0\)
ΔOBC cân tại O
=>\(\widehat{OBC}=\widehat{OCB}=\dfrac{180^0-120^0}{2}=30^0\)
gíup e vs ạ hiu hiu 
13 tháng 8 2019
bài 1
P=\(\left(\frac{x+2}{x\sqrt{x}-1}+\frac{\sqrt{x}}{x+\sqrt{x}+1}-\frac{1}{\sqrt{x}-1}\right)\)
=\(\left(\frac{x+2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}+\frac{\sqrt{x}\left(\sqrt{x}-1\right)}{...}-\frac{\left(x+\sqrt{x}+1\right)}{...}\right):\frac{\sqrt{x}-1}{2}\)
=\(\left(\frac{x+2+x-\sqrt{x}-x-\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\right):\frac{\sqrt{x}-1}{2}\)
=\(\left(\frac{x-2\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\right):\frac{\sqrt{x}-1}{2}\)
=\(\left(\frac{\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\right):\frac{\sqrt{x}-1}{2}\)
=\(\frac{\sqrt{x}-1}{x+\sqrt{x}+1}.\frac{2}{\sqrt{x}-1}\)
=\(\frac{2}{x+\sqrt{x}+1}\)
P>0 dựa vào dkxd
13 tháng 8 2019
Bài 1:
a) P= \(\left(\frac{x+2}{x\sqrt{x}-1}+\frac{\sqrt{x}}{x+\sqrt{x}+1}+\frac{1}{1-\sqrt{x}}\right):\frac{\sqrt{x}-1}{2}\) (x ≥ 0; x ≠ 4)
=\(\left(\frac{x+2}{\left(\sqrt{x}-1\right)\cdot\left(x+\sqrt{x}+1\right)}+\frac{\left(\sqrt{x}-1\right)\cdot\sqrt{x}}{\left(\sqrt{x}-1\right)\cdot\left(x+\sqrt{x}+1\right)}-\frac{x+\sqrt{x}+1}{\left(\sqrt{x}-1\right)\cdot\left(x+\sqrt{x}+1\right)}\right)\cdot\frac{2}{\sqrt{x}-1}\)
= \(\left(\frac{x+2+x-\sqrt{x}-x-\sqrt{x}-1}{\left(\sqrt{x}-1\right)\cdot\left(x+\sqrt{x}+1\right)}\right)\cdot\frac{2}{\sqrt{x}-1}\)
=\(\left(\frac{x-2\sqrt{x}+1}{\left(\sqrt{x}-1\right)\cdot\left(x+\sqrt{x}+1\right)}\right)\cdot\frac{2}{\sqrt{x}-1}\)
=\(\frac{\left(\sqrt{x}-1\right)^2\cdot2}{\left(\sqrt{x}-1\right)\cdot\left(x+\sqrt{x}+1\right)\cdot\left(\sqrt{x}-1\right)}\)
=\(\frac{2}{x+\sqrt{x}+1}\)
b) Ta có: x ≥ 0 ⇒ \(\sqrt{x}\) ≥ 0
⇒ \(x+\sqrt{x}+1\) ≥ 1 > 0
mà 2 > 0 ⇒ \(\frac{2}{x+\sqrt{x}+1}\) > 0 ⇒ P > 0
Bài 2:
a) P= \(\left(\frac{2\sqrt{x}+x}{x\sqrt{x}-1}-\frac{1}{\sqrt{x}-1}\right):\left(1-\frac{\sqrt{x}+2}{x+\sqrt{x}+1}\right)\) (x ≥ 0; x ≠ 1)
=\(\left(\frac{2\sqrt{x}+x}{\left(\sqrt{x}-1\right)\cdot\left(x+\sqrt{x}+1\right)}-\frac{x+\sqrt{x}+1}{\left(\sqrt{x}-1\right)\cdot\left(x+\sqrt{x}+1\right)}\right):\left(\frac{x+\sqrt{x}+1}{x+\sqrt{x}+1}-\frac{\sqrt{x}+2}{x+\sqrt{x}+1}\right)\)
=\(\left(\frac{2\sqrt{x}+x-x-\sqrt{x}-1}{\left(\sqrt{x}-1\right)\cdot\left(x+\sqrt{x}+1\right)}\right):\left(\frac{x+\sqrt{x}+1-\sqrt{x}-2}{x+\sqrt{x}+1}\right)\)
=\(\left(\frac{\sqrt{x}-1}{\left(\sqrt{x}-1\right)\cdot\left(x+\sqrt{x}+1\right)}\right):\left(\frac{x-1}{x+\sqrt{x}+1}\right)\)
=\(\frac{\sqrt{x}-1}{\left(\sqrt{x}-1\right)\cdot\left(x+\sqrt{x}+1\right)}\cdot\frac{x+\sqrt{x}+1}{x-1}\)
=\(\frac{1}{x-1}\)
b) Ta có: \(\sqrt{P}=\sqrt{\frac{1}{x-1}}\)
= \(\frac{1}{\sqrt{x-1}}\)
x = \(5+2\sqrt{3}\) (TM)
Thay x vào \(\sqrt{P}\) ta có:
\(\sqrt{P}=\frac{1}{\sqrt{5+2\sqrt{3}-1}}\)
=\(\frac{1}{\sqrt{4+2\sqrt{3}}}\)
=\(\frac{1}{\sqrt{3+2\sqrt{x}+1}}\)
=\(\frac{1}{\sqrt{\left(\sqrt{3}+1\right)^2}}\)
=\(\frac{1}{\left|\sqrt{3}+1\right|}\)
=\(\frac{1}{\sqrt{3}+1}\)
= \(\frac{\sqrt{3}-1}{\left(\sqrt{3}+1\right)\cdot\left(\sqrt{3}-1\right)}\)
=\(\frac{\sqrt{3}-1}{2}\)
Vậy \(\sqrt{P}=\frac{\sqrt{3}-1}{2}\) khi x = \(5+2\sqrt{3}\)
DD
5
17 tháng 7 2017
Ta có \(P=\left(\frac{\sqrt{14}-\sqrt{7}}{\sqrt{8}-2}-\frac{\sqrt{15}-\sqrt{3}}{2-2\sqrt{5}}\right):\frac{1}{\sqrt{7}-\sqrt{3}}\)
\(=\left(\frac{\sqrt{7}\left(\sqrt{2}-1\right)}{2\left(\sqrt{2}-1\right)}-\frac{\sqrt{3}\left(\sqrt{5}-1\right)}{2\left(1-\sqrt{5}\right)}\right).\left(\sqrt{7}-\sqrt{3}\right)\)
\(=\left(\frac{\sqrt{7}}{2}+\frac{\sqrt{3}}{2}\right).\left(\sqrt{7}-\sqrt{3}\right)=\frac{\sqrt{7}+\sqrt{3}}{2}.\left(\sqrt{7}-\sqrt{3}\right)\)
\(=\frac{7-3}{2}=2\)
Vậy \(P=2\)