Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Minh goi y thoi nhe muon roi mik chuan bi di ngu bn thong cam
a) ban dung dinh nghia tiep tuyen la xong
b) cm O la truc tam tam giac BAN roi dung yeu to // la ok
c) mik nghi la : de thay Samn=1/2 Sabc (t/c trung tuyen.....)
thi Samn Min <=> Sabc min
Cau c) mik ko chac lam co cau a,b ban cu lam theo mik kieu gi cung ra
Co gi de mai mik ngu day mik lam cho
a) Xet \(\Delta ADE\) co AO=DO=EO=R => DE la duong kinh (O)
Ta co MD cat (O) duy nhat tai D=> MD la tiep tuyen (O)=> \(MD\perp DE\)
Tuong tu NE la tiep tuyen (O) =>\(NE\perp DE\)
Suy ra MD//NE ( Quan he tu vuong goc den song song)
b) Noi NO , Goi F la trung diem OH
Xet \(\Delta AHC\) co OH=OA ( gt) , HN=NC (gt)
=> ON la duong trung binh => ON//AC
ma AB \(AB\perp AC\left(\Delta ABCvuong\right)\)
Suy ra \(NO\perp AB\)
Xet tam giac ABN co \(AH\perp BN\left(gt\right),NO\perp AB\left(cmt\right)\) => O la truc tam tam giac ABN
=> \(BO\perp AN\) (1)
Xet tam giac giac BHO co M la trung diem BH (gt) , F la trung diem OH ( gt)
=> MF la duong trung binh => MF//BO (2)
Tu (1) va (20 suy ra \(MF\perp AN\) (quan he tu vuong goc den song song)
Xet tam giac AMN co \(\hept{\begin{cases}AH\perp MN\left(gt\right)\\MF\perp AN\left(cmt\right)\end{cases}\Rightarrow}\) Trung diem F cua OH la truc tam \(\Delta AMN\)
c) Xet tam giac ABH co AM la duong trung tuyen =>Samh =Sabm ( t/c trug tuyen chia cat doi dien thang 2 phan co dien h bag nhau)
=> Samh=1/2Sabh
tuong tu ta cung co Sahn = 1/2 Sahc
Suy ra Samh+Sahn =1/2 (Sabh +Sahc)
<=> Samn=1/2 Sabc
=> Samn min <=> Sabc min
Theo minh thi tam giac ABC can co dk la dien h tam giac ABC nho nhat thi Samn dat gtnn
Mik ko chac cau c) lam dau. Neu sai mong cac bn thong cam ma sua ho mik,Mik cam on.
Chuc ban hoc tot
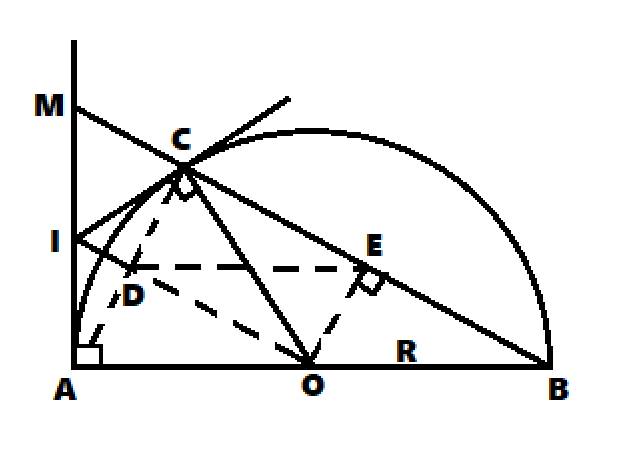
a: Xét tứ giác IAOC có
\(\widehat{IAO}+\widehat{ICO}=90^0+90^0=180^0\)
=>IAOC là tứ giác nội tiếp
=>I,A,O,C cùng thuộc một đường tròn
b: Xét (O) có
IA,IC là tiếp tuyến
Do đó: IA=IC
=>I nằm trên đường trung trực của AC(1)
ta có: OA=OC
=>O nằm trên đường trung trực của AC(2)
Từ (1) và (2) suy ra OI là đường trung trực của AC
=>OI\(\perp\)AC
c: Xét (O) có
ΔCAB nội tiếp
AB là đường kính
Do đó: ΔCAB vuông tại C
Ta có: OI là đường trung trực của AC
=>OI vuông góc với AC tại trung điểm của AC
mà OI cắt AC tại D
nên OI\(\perp\)AC tại D và D là trung điểm của AC
Xét tứ giác CDOE có
\(\widehat{CDO}=\widehat{CEO}=\widehat{ECD}=90^0\)
=>CDOE là hình chữ nhật
=>CO=DE=R
d: Xét ΔIAC có IA=IC
nên ΔIAC cân tại I
=>\(\widehat{IAC}=\widehat{ICA}\)
Ta có: ΔACB vuông tại C
=>AC\(\perp\)CB tại C
=>AC\(\perp\)MB tại C
=>ΔACM vuông tại C
Ta có: \(\widehat{IAC}+\widehat{IMC}=90^0\)(ΔACM vuông tại C)
\(\widehat{ICA}+\widehat{ICM}=\widehat{ACM}=90^0\)
mà \(\widehat{IAC}=\widehat{ICA}\)
nên \(\widehat{IMC}=\widehat{ICM}\)
=>IM=IC
mà IC=IA
nên IM=IA
=>I là trung điểm của MA
=>\(MA=2\cdot IC\)
Xét ΔABM vuông tại A có AC là đường cao
nên \(MC\cdot MB=MA^2\)
=>\(MC\cdot MB=\left(2\cdot IC\right)^2=4\cdot IC^2\)
=>\(IC^2=\dfrac{1}{4}\cdot MC\cdot MB\)