
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a)
=
= -4.
b)
=
=
(2-x) = 4.
c)
=
=
=
=
.
d)
=
= -2.
e)
= 0 vì
(x2 + 1) =
x2( 1 +
) = +∞.
f)
=
= -∞, vì
> 0 với ∀x>0.

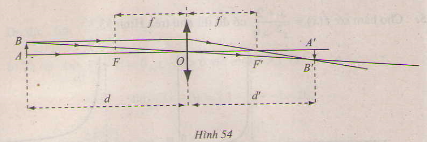
a) Từ hệ thức suy ra d' = φ(d) =
.
b) +) φ(d) =
= +∞ .
Ý nghĩa: Nếu vật thật AB tiến dần về tiêu điểm F sao cho d luôn lớn hơn f thì ảnh của nó dần tới dương vô cực.
+) φ(d) =
= -∞.
Ý nghĩa: Nếu vật thật AB tiến dần về tiêu điểm F sao cho d luôn nhỏ hơn f thì ảnh của nó dần tới âm vô sực.
+) φ(d) =
=
= f.
Ý nghĩa: Nếu vật thật AB ở xa vô cực so với thấu kính thì ảnh của nó ở ngay trên tiêu diện ảnh (mặt phẳng qua tiêu điểm ảnh F' và vuông góc với trục chính).

+) Hàm số f(x) = xác định khi và chỉ khi x2+ x - 6 ≠ 0 <=> x ≠ -3 và x ≠ 2.
Hàm số f(x) liên tục trên các khoảng (-∞; -3), (-3; 2) và (2; +∞)
+) Hàm số g(x) = tanx + sinx xác định khi và chỉ khi
tanx ≠ 0 <=> x ≠ +kπ với k ∈ Z.
Hàm số g(x) liên tục trên các khoảng ( - +kπ;
+kπ) với k ∈ Z.

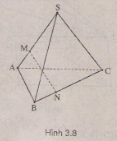
=
+
+
= +
+
(1)
=
+
+
= +
+
(2)
Nhân (2) với 2 rồi cộng với (1) ta được: =
+
Vậy ,
,
đồng phẳng.

a) Ta có g(x) =
=
(x2 + 2x + 4) = 22 +2.2 +4 = 12.
Vì g(x) ≠ g(2) nên hàm số y = g(x) gián đoạn tại x0 = 2.
b) Để hàm số y = f(x) liên tục tại x0 = 2 thì ta cần thay số 5 bởi số 12.

a) Học sinh tự vẽ hình. Đồ thị hàm số y = f(x) là một đường không liền nét mà bị đứt quãng tại x0 = -1. Vậy hàm số đã cho liên tục trên khoảng (-∞; -1) và (- 1; +∞).
b) +) Nếu x < -1: f(x) = 3x + 2 liên tục trên (-∞; -1) (vì đây là hàm đa thức).
+) Nếu x> -1: f(x) = x2 - 1 liên tục trên (-1; +∞) (vì đây là hàm đa thức).
+) Tại x = -1;
Ta có f(x) =
(3x + 2) = 3(-1) +2 = -1.
f(x) =
(x2 - 1) = (-1)2 - 1 = 0.
Vì f(x) ≠
f(x) nên không tồn tại
f(x). Vậy hàm số gián đoạn tại
x0 = -1.
a) Hàm số f(x) = xác định trên R\{
xác định trên R\{ } và ta có x = 4 ∈ (
} và ta có x = 4 ∈ ( ;+∞).
;+∞).
Giả sử (xn) là dãy số bất kì và xn ∈ ( ;+∞); xn ≠ 4 và xn → 4 khi n → +∞.
;+∞); xn ≠ 4 và xn → 4 khi n → +∞.
Ta có lim f(xn) = lim =
=  =
=  .
.
Vậy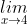
 =
=  .
.
b) Hàm số f(x) = xác định trên R.
xác định trên R.
Giả sử (xn) là dãy số bất kì và xn → +∞ khi n → +∞.
Ta có lim f(xn) = lim = lim
= lim  = -5.
= -5.
Vậy
 = -5.
= -5.