Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn Click vô để tham khảo nhé:
Câu hỏi của Ho Pham Phu An - Toán lớp 7 - Học toán với OnlineMath

Gọi số tiền vốn lần lượt là a,b,c(đồng)
Đk:a,b,c<450
a,b,c thuộc N*
Theo bài ra, ta có:
a/3=b/5=c/7 và a+b+c=450
Theo tính chất dãy tỉ số bằng nhau, ta có:
a/3=b/5=c/7=a+b+c/3+5+7=450/15=30
Với:
a/3=30=>a=3.30=90
b/5=30=>b=5.30=150
c/7=30=>c=7.30=210

Giải:
Gọi số tiền thiết kế, xây thô, hoàn thiện là a, b, c ( a, b, c \(\in\) N* )
Ta có: \(\frac{a}{2}=\frac{b}{36}=\frac{c}{62}\) và c - ( a + b ) = 180
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{a}{2}=\frac{b}{36}=\frac{c}{62}=\frac{c-\left(a+b\right)}{62-\left(2+36\right)}=\frac{180}{24}=7,5\)
+) \(\frac{a}{2}=7,5\Rightarrow a=15\)
+) \(\frac{b}{36}=7,5\Rightarrow b=270\)
+) \(\frac{c}{62}=7,5\Rightarrow c=465\)
Vậy số tiền thiết kế là 15 triệu đồng
số tiền xây thô là 270 triệu đồng
số tiền hoàn thiện là 465 triệu đồng
Gọi số tiền thiết kế, xây thô, hoàn thiện lần lượt là x,y,z
(x,y,z ϵ N*)
Theo bài ta có: x : y : z = 2 : 36 : 62
hay \(\frac{x}{2}\) = \(\frac{y}{36}\) = \(\frac{z}{62}\) và z - (x + y) = 180
Theo tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{x}{2}\) = \(\frac{y}{36}\) = \(\frac{z}{62}\) = \(\frac{z-\left(x+y\right)}{62-\left(2+36\right)}\) = \(\frac{180}{24}\) = 7,5
\(\Rightarrow\) \(\left[\begin{array}{nghiempt}x=7,5.2\\y=7,5.36\\z=7,5.62\end{array}\right.\) \(\Rightarrow\) \(\left[\begin{array}{nghiempt}x=15\\y=270\\z=465\end{array}\right.\)
Vây số tiền thiết kế là: 15 triệu đồng
xây thô là: 270 triệu đồng
hoàn thiện là: 465 triệu đồng

\(\text{Gọi x;y;z lần lượt là số tiền lớp 7A,7B,7C}\)
(đk:x;y;z\(\in\)N*,đơn vị:triệu đồng)
\(\text{Ta có:}\dfrac{x}{4}=\dfrac{y}{5}=\dfrac{z}{6}\text{ và }x+y+z=30\)
\(\text{Áp dụng tính chất dãy tỉ số bằng nhau:}\)
\(\dfrac{x}{4}=\dfrac{y}{5}=\dfrac{z}{6}=\dfrac{x+y+z}{4+5+6}=\dfrac{30}{15}=2\)
\(\Rightarrow x=2.4=8\text{(triệu đồng)}\)
\(y=2.5=10\text{(triệu đồng)}\)
\(z=2.6=12\text{(triệu đồng)}\)
\(\text{Vậy số tiền lớp 7A là:8 triệu đồng}\)
\(\text{lớp 7B là:10 triệu đồng}\)
\(\text{ lớp 7C là:12 triệu đồng}\)

Gọi số vốn của 3 đơn vị lần lượt là a,b,c
Ta có : a : b : c = 3 : 5 : 7
\(\Rightarrow\dfrac{a}{3}=\dfrac{b}{5}=\dfrac{c}{7}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có :
\(\Rightarrow\dfrac{a}{3}=\dfrac{b}{5}=\dfrac{c}{7}=\dfrac{a+b+c}{3+5+7}=\dfrac{450}{15}=30\)
\(\Rightarrow a=30.3=90\)
\(b=30.5=150\)
\(c=30.7=210\)
Vậy số tiền lãi lần lượt của 3 đơn vị là 90 triệu , 150 triệu và 210 triệu ( đồng )

Gọi a,b,c (triệu đồng) lần lượt là số tiền lãi của 3 đơn vị (0 < a, b, c < 450).
Tổng số tiền lãi là 450 triệu đồng nên a+b+c = 450
Vì số tiền lãi tỉ lệ thuận với số vốn đã góp nên ta có:
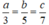
Theo tính chất của dãy tỉ số bằng nhau ta có:
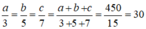
a/3 = 30 ⇒ a = 3.30 = 90
b/5 = 30 ⇒ b = 5.30 = 150
c/7 = 30 ⇒ c = 7.30 = 210
Vậy số tiền lãi được chia cho các đơn vị theo thứ tự là 90 triệu; 150 triệu và 210 triệu
Gọi số tiền nhà từ thiện thứ nhất, thứ hai và thứ ba đã đóng góp lần lượt là x, y, z (triệu đồng).
Do ba nhà từ thiện đóng góp số tiền theo tỉ lệ 3 : 5 : 7 nên x3=y5=z7.
Do tổng số tiền từ thiện là 450 triệu đồng nên x + y + z = 450.
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{3}\)=\(\dfrac{y}{5}\)=\(\dfrac{z}{7}\)=\(\dfrac{x+y+z}{3+5+7}\)=\(\dfrac{450}{15}\)= 30
Do đó x = 3.30 = 90, y = 5.30 = 150, z = 7.30 = 210.
=> số tiền đóng góp của ba nhà từ thiện lần lượt là 90 triệu đồng, 150 triệu đồng và 210 triệu đồng.