Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nếu lấy trung bình cộng 3 số a, b,c thì ta được kết quả: \(\frac{a+b+c}{3}\)
Nếu lấy trung bình cộng của a và b, rồi lấy trung bình cộng của kết quả này với c, ta được kết quả: \(\frac{\frac{a+b}{2}+{c}}{2}\)
Ta xét biểu thức \(\frac{a+b+c}{3}-\frac{\frac{a+b}{2}+{c}}{2}=\frac{a+b+c}{3} - \frac{a+b+2c}{4}=\frac{4a+4b+4c-3a-3b-6c}{12}=\frac{a+b-2c}{12}\)
Đến đây, vì \(a>b>c \Rightarrow a+b>2c \iff a+b-2c>0 \iff \frac{a+b-2c}{12}>0\)
Từ đây ta có thể suy ra \(\frac{a+b+c}{3}>\frac{\frac{a+b}{2}+c}{2} \Rightarrow đpcm\)

cách tính trên sai
chỉ cần lấy (a+b+c):3 là ok
tick cko mình nhé

d. Số trung bình cộng: X = (7.4 + 8.8 + 9.10 + 10.8)/30 = 8,73 (1 điểm)
Mốt của dấu hiệu là: Mo = 9 (1 điểm)

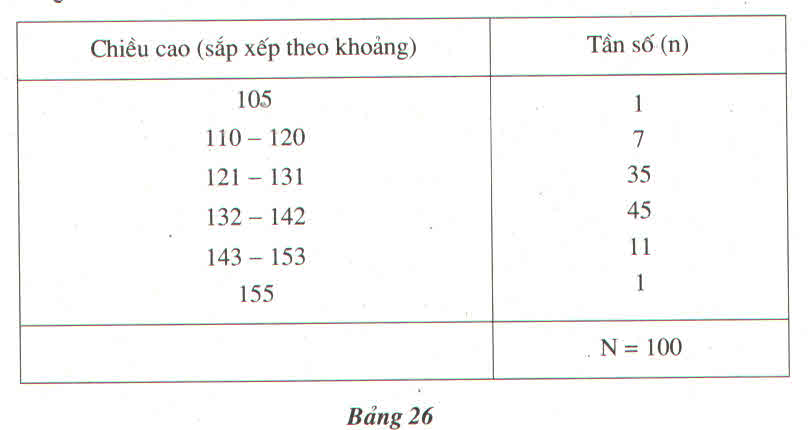
a) Bảng này có khác so với bảng tần số đã học.
Các giá trị khác nhau của biến lượng được "phân lớp" trong các lớp đều nhau (10 đơn vị) mà không tính riêng từng giá trị khác nhau.
b) Số trung bình cộng
Để tiện việc tính toán ta kẻ thêm vào sau cột chiều cao là cột số trung bình cộng của từng lớp; sau cột tần số là cột tích giữa trung bình cộng.
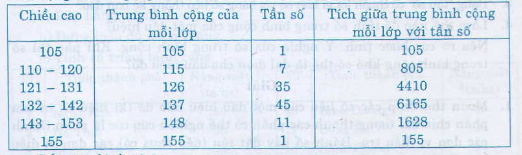
Số trung bình cộng:\(\overline{X}=\dfrac{105+805+4410+6165+1628+155}{100}=132,68\left(cm\right)\)
a) Bảng này có khác so với bảng tần số đã học.
Các giá trị khác nhau của biến lượng được "phân lớp" trong các lớp đều nhau (10 đơn vị) mà không tính riêng từng giá trị khác nhau.
b) Số trung bình cộng
Để tiện việc tính toán ta kẻ thêm vào sau cột chiều cao là cột số trung bình cộng của từng lớp; sau cột tần số là cột tích giữa trung bình cộng.

Số trung bình cộng:¯¯¯¯¯X=105+805+4410+6165+1628+155100=132,68(cm)
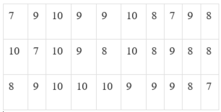
Cách tính đúng là: \(\frac{a+b+c}{3}\)
Cách tính của bạn An là: \(\frac{\frac{a+b}{2}+c}{2}=\frac{a+b+2c}{4}\)
Ta có: \(\frac{a+b+c}{3}\)\(-\frac{a+b+2c}{4}\)
\(=\frac{4a+4b+4c-3a-3b-6c}{12}\)
\(=\frac{a+b-2c}{12}=\frac{\left(a-c\right)+\left(b-c\right)}{12}>0\)(vì a > b > c)
Vậy \(\frac{a+b+c}{3}\)\(>\frac{a+b+2c}{4}\)
=> đpcm...