K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

HP
26 tháng 1 2021
Đồ thị hàm số \(y=f\left(\left|x\right|\right)\)
\(f^2\left(\left|x\right|\right)+\left(m-1\right)f\left(\left|x\right|\right)-m=0\left(1\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}f\left(\left|x\right|\right)=1\left(2\right)\\f\left(\left|x\right|\right)=-m\left(3\right)\end{matrix}\right.\)
Từ đồ thị ta thấy phương trình \(\left(2\right)\) có hai nghiệm phân biệt nên phương trình \(\left(1\right)\) có hai nghiệm phân biệt khi phương trình \(\left(3\right)\) có hai nghiệm phân biệt khác hai nghiệm của phương trình \(\left(2\right)\).
\(\Leftrightarrow\left[{}\begin{matrix}-m=-3\\-1< -m< 1\\-m>1\end{matrix}\right.\)
...
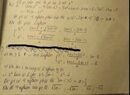

Điều kiện xác định x∈Rx∈R.
Đặt t=√x2+1 (t≥1t≥1)
Phương trình trở thành t2−1−4t−m+1=0
⇔t2−4t=m
⇔t2−4t=m. (1)
Để phương trình có 44 nghiệm phân biệt thì phương trình (1) có hai nghiệm phân biệt lớn hơn 11.
Xét hàm số f(t)=t2−4t có đồ thị là parabol có hoành độ đỉnh x=2∈(1;+∞) nên ta có bảng biến thiên:
Dựa BBT ta thấy để (1) có hai nghiệm phân biệt lớn hơn 11 thì −4<m<−3
Vậy không có giá trị nguyên của mm thỏa mãn yêu cầu bài toán.
mik có ghi thừa 1 dòng ⇔t2-4t=m bạn nhé