BN
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NH
1
21 tháng 7 2023
-3x^2+2x-1
=-3(x^2-2/3x+1/3)
=-3(x^2-2*x*1/3+1/9+2/9)
=-3(x-1/3)^2-2/3<=-2/3<0 với mọi x
P
1
9 tháng 11 2016
\(x^4+2x^3-3x^2-4x+4=\left(x^4+2x^3+x^2\right)-4\left(x^2+x\right)+4\)
\(=\left(x^2+x\right)^2-4\left(x^2+x\right)+4=\left(x^2+x-2\right)^2\ge0\)
\(\Rightarrow\)ĐPCM
13 tháng 6 2019
Bài 1
\(a,\)\(49x^2-28x+7\)
\(=\left(7x\right)^2-2.7x.2+2^2+3\)
\(=\left(7x-2\right)^2+3\ge3\)( luôn dương )
Dấu bằng sảy ra khi và chỉ khi \(\left(7x-2\right)^2=0\)
\(\Rightarrow7x-2=0\)
\(\Rightarrow x=\frac{2}{7}\)
13 tháng 6 2019
Bài 1 b
\(x^2+\frac{2}{5}x+\frac{1}{5}\)
\(=x^2+2.x.\frac{1}{5}+\frac{1}{25}+\frac{4}{25}\)
\(=\left(x+\frac{1}{5}\right)^2+\frac{4}{25}\ge\frac{4}{25}\)( luôn dương )
Dấu bằng sảy ra khi và chỉ khi \(\left(x+\frac{1}{5}\right)^2=0\)
\(\Rightarrow x+\frac{1}{5}=0\)
\(\Rightarrow x=-\frac{1}{5}\)
A
30 tháng 6 2021
Bài 1
\(A=x^2-6x+15=x^2-2.3.x+9+6=\left(x-3\right)^2+6>0\forall x\)
\(B=4x^2+4x+7=\left(2x\right)^2+2.2.x+1+6=\left(2x+1\right)^2+6>0\forall x\)
Bài 2
\(A=-9x^2+6x-2021=-\left(9x^2-6x+2021\right)=-\left[\left(3x-1\right)^2+2020\right]=-\left(3x-1\right)^2-2020< 0\forall x\)
1 tháng 10 2021
(1-2x)(x-1)-5
=-2x2+3x-1-5
=-2x2+3x-6
=-2(x2-3/2x+3)
=-2(x-3/4)2-39/8
Vì (x-3/4)2≥0 với mọi x
⇒-2(x-3/4)2≤0
⇒-2(x-3/4)2-39/8<0
Vậy biểu thức (1-2x)(x-1)-5 luôn âm với mọi x
S
6 tháng 7 2018
1/
\(M=3x^2-4x+3=3\left(x^2-\frac{4}{3}x+1\right)=3\left(x^2-2x\cdot\frac{2}{3}+\frac{4}{9}\right)+\frac{5}{3}=3\left(x-\frac{2}{3}\right)^2+\frac{5}{3}\ge\frac{5}{3}>0\)
\(N=5x^2-10x+2018=5\left(x^2-2x+1\right)+2013=5\left(x-1\right)^2+2013\ge2013>0\)
\(P=x^2+2y^2-2xy+4y+7=\left(x^2-2xy+y^2\right)+\left(y^2+4y+4\right)+3=\left(x-y\right)^2+\left(y+2\right)^2+3\ge3>0\)
2/
\(A=10x-6x^2+7=-6x^2+10x+7=-6\left(x^2-\frac{10}{6}x+\frac{25}{36}\right)-\frac{11}{6}=-6\left(x-\frac{5}{6}\right)^2-\frac{11}{6}\le-\frac{11}{6}< 0\)
\(B=-3x^2+7x+10=-3\left(x^2-\frac{7}{3}x+\frac{49}{36}\right)-\frac{311}{12}=-3\left(x-\frac{7}{6}\right)^2-\frac{311}{12}\le-\frac{311}{12}< 0\)
\(C=2x-2x^2-y^2+2xy-5=\left(2x-x^2-1\right)-\left(x^2-2xy+y^2\right)-4=-\left(x^2-2x+1\right)-\left(x-y\right)^2-4=-\left(x-1\right)^2-\left(x-y\right)^2-4\)\(\le-4< 0\)
19 tháng 8 2017
a)\(-\frac{1}{4}x^2+x-2=-\left[\left(\frac{1}{2}x\right)^2-2.\frac{1}{2}x+1+1\right]\)
\(=-1-\left(\frac{1}{2}x-1\right)^2\le-1\left(đpcm\right)\)
b)\(-3x^2-6x-9=-3\left(x^2-2x+1+2\right)\)
\(=-6-3\left(x-1\right)^2\le-6\left(đpcm\right)\)
19 tháng 8 2017
c)\(-2x^2+3x-6=-2\left(x^2-\frac{3}{2}x+3\right)\)
\(=-2\left(x^2-2.\frac{3}{4}x+\frac{9}{16}+\frac{39}{16}\right)\)
\(=-\frac{39}{8}-2\left(x-\frac{3}{4}\right)^2\le-\frac{39}{8}\)
d) tương tự
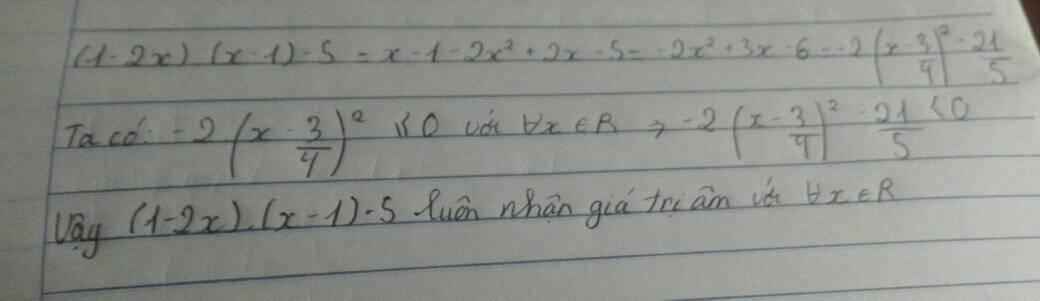
em ko biết,em mới lớp 5 thui mừ
Ta có: \(3x^2+2x-5=3\left(x^2+\frac{2}{3}x-\frac{5}{3}\right)\)
\(=3\left(x^2+2.\frac{1}{3}x+\frac{1}{9}-\frac{16}{9}\right)\)
\(=3\left[\left(x+\frac{1}{3}\right)^2-\frac{16}{9}\right]\)
\(=3\left(x+\frac{1}{3}\right)^2-\frac{16}{3}\ge\frac{-16}{3}\left(????\right)\)