Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(S_{DEF}=\dfrac{EH\cdot DF}{2}=\dfrac{ED\cdot EF}{2}\)
nên \(EH\cdot DF=ED\cdot EF\)
b: \(DF=\sqrt{15^2+20^2}=25\left(cm\right)\)
\(EH=\dfrac{15\cdot20}{25}=12\left(cm\right)\)
c: Xét ΔDEF vuông tại E có EH là đường cao
nên \(EF^2=DF\cdot HF\)
d: Xét ΔEHD vuông tại H có HM là đường cao
nên \(EM\cdot ED=EH^2\left(1\right)\)
Xét ΔEHF vuông tại H có HN là đường cao
nên \(EN\cdot EF=EH^2\left(2\right)\)
Từ (1) và (2) suy ra \(EM\cdot ED=EN\cdot EF\)
hay EM/EF=EN/ED
Xét ΔEMN và ΔEFD có
EM/EF=EN/ED
góc MEN chung
Do đo: ΔEMN đồng dạng với ΔEFD

a: Xét ΔDEF vuông tại E cso EH là đường cao
nên \(EH\cdot DF=ED\cdot EF\)(hệ thức lượng)
\(DF=\sqrt{15^2+20^2}=25\left(cm\right)\)
\(EH=\dfrac{ED\cdot EF}{DF}=\dfrac{15\cdot20}{25}=12\left(cm\right)\)
b: Xét ΔEHD vuông tại H có HM là đường cao
nên \(EM\cdot ED=EH^2\left(1\right)\)
Xét ΔEHF vuông tại H có HN là đường cao
nên \(EN\cdot EF=EH^2\left(2\right)\)
Từ (1) và (2) suy ra \(EM\cdot ED=EN\cdot EF\)
hay EM/EF=EN/ED
Xét ΔEMN vuông tại E và ΔEFD vuông tại E có
EM/EF=EN/ED
Do đó ΔEMN\(\sim\)ΔEFD

Câu 1:
a: \(S_{EDF}=\dfrac{EH\cdot DF}{2}=\dfrac{ED\cdot EF}{2}\)
nên \(EH\cdot DF=ED\cdot EF\)
\(DF=\sqrt{15^2+20^2}=25\left(cm\right)\)
\(EH=\dfrac{ED\cdot EF}{FD}=12\left(cm\right)\)
b: Xét ΔEHD vuông tại H có HM là đường cao
nên \(EM\cdot ED=EH^2\left(1\right)\)
Xét ΔEHF vuông tại H có HN là đường cao
nên \(EN\cdot EF=EH^2\left(2\right)\)
Từ (1) và (2) suy ra \(EM\cdot ED=EN\cdot EF\)
hay EM/EF=EN/ED
=>ΔEMN\(\sim\)ΔEFD

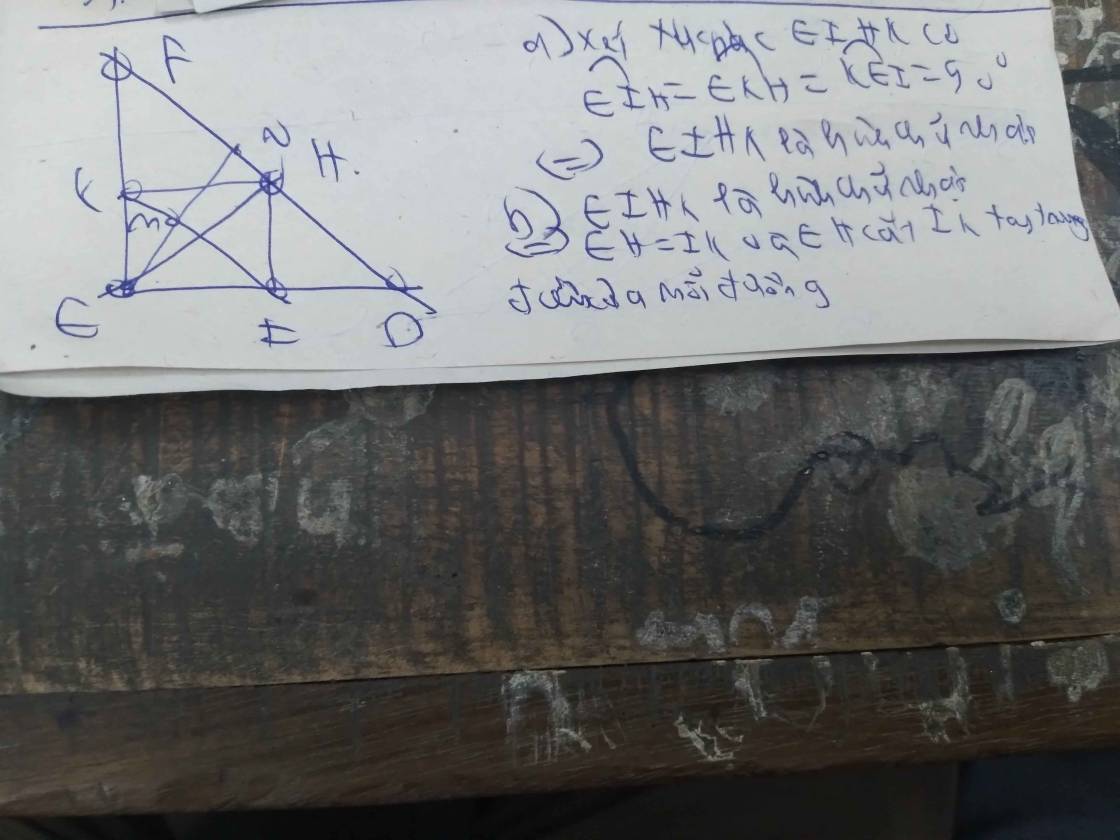
a) xét ΔHED và ΔDEF có
\(\widehat{EHD}=\widehat{EDF}=\)90o
\(\widehat{E} chung\)
=> ΔHED ∼ ΔDEF (gg)
b) Xét ΔDEF có \(\widehat{D}=\)90o
=> DE2+DF2=EF2
=>62+82=EF2
=> EF=10 cm
SΔDEF=\(\dfrac{ED.DF}{2}=\dfrac{DH.EF}{2}\)=> ED.DF=DH.EF => 6.8=DH.10
=> DH =4,8 cm
c) Xét ΔDEH có \(\widehat{EHD}=90\)o
=> HD2.HE2=ED2
=>4.82+HE2=62
=> HE=3.6
ta lại có DI là phân giác
=> \(\dfrac{EI}{IH}=\dfrac{ED}{HD}\)
=>\(\dfrac{EI}{EH-EI}=\dfrac{6}{4.8} \)=>\(\dfrac{EI}{3.6-EI}=\dfrac{6}{4.8}\)=>EI=2
=> IH=EH-EI=3.6-2=1.6
a) Xét ΔHED vuông tại H và ΔDEF vuông tại D có
\(\widehat{HED}\) chung
Do đó: ΔHED\(\sim\)ΔDEF(g-g)

a: \(EF=\sqrt{6^2+8^2}=10\left(cm\right)\)
Xet ΔEDF có EK là phân giác
nên DK/DE=FK/FE
=>DK/3=FK/5=(DK+FK)/(3+5)=8/8=1
=>DK=3cm; FK=5cm
b: Xet ΔDEK vuông tại D và ΔHEI vuông tại H có
góc DEK=góc HEI
=>ΔDEK đồng dạng với ΔHEI
=>ED/EH=EK/EI
=>ED*EI=EK*EH
c: góc DKI=90 độ-góc KED
góc DIK=góc HIE=90 độ-góc KEF
mà góc KED=góc KEF
nên góc DKI=góc DIK
=>ΔDKI cân tại D
mà DG là trung tuyến
nên DG vuông góc IK

E M N H F
a) EH là phân giác nên ta có:
\(\frac{HM}{HN}=\frac{EM}{EN}=\frac{3}{4}\)
b) Áp dụng định lí pitago cho tam giác EMN vuông tại E ta có:
\(MN^2=ME^2+EN^2=25\Rightarrow MN=5\)
c) Ta có: \(HM=\frac{3}{4}HN\)
Mặt khác: HM+HN=MN=5=> \(\frac{3}{4}HN+HN=5\Leftrightarrow HN=\frac{20}{7}\)và \(HM=\frac{3}{4}.\frac{20}{7}=\frac{15}{7}\)
d) Xét tam giác EMN vuông tại E và tam giác FHN vuông tại H có góc N chung
suy ra hai tam giác này đồng dạng theo trường hợp góc góc

E D F H K M N I
Bài làm
a) Xét tam giác DEH và tam giác DEF có:
\(\widehat{DHE}=\widehat{DEF}\left(=90^0\right)\)
\(\widehat{D}\) chung
=> Tam giác DEH ~ Tam giác DEF ( g - g )
=> \(\frac{DE}{DF}=\frac{HE}{EF}\)
\(\Rightarrow DE.EF=DF.EH\) ( đpcm )
b) Xét tam giác DEF vuông tại E có:
DF2 = DE2 + EF2
hay DF2 = 152 + 202
=> DF2 = 225 + 400
=> DF2 = 625
=> DF = 25 ( cm )
Vì tam giác DEH ~ Tam giác DEF ( cmt )
=> \(\frac{DH}{DE}=\frac{DE}{DF}\)
hay \(\frac{DH}{15}=\frac{15}{25}\Rightarrow DH=9\left(cm\right)\)
Ta có: DH + HF = DF
hay 9 + HF = 25
=> HF = 16 ( cm )
c) Xét tam giác HEF và tam giác EDF có:
\(\widehat{EHF}=\widehat{DEF}\left(=90^0\right)\)
\(\widehat{F}\) chung
=> Tam giác HEF ~ Tam giác EDF ( g - g )
=> \(\frac{EF}{DF}=\frac{HF}{EF}\Rightarrow EF^2=DF.HF\) ( đpcm )