Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét ΔABC có
\(BC^2=AB^2+AC^2\left(5^2=3^2+4^2\right)\)
nên ΔABC vuông tại A(Định lí Pytago đảo)
Xét ΔABC vuông tại A có
\(\sin\widehat{C}=\dfrac{AB}{BC}=\dfrac{4}{5}\)
nên \(\widehat{C}\simeq53^0\)
\(\Leftrightarrow\widehat{B}=37^0\)
b) Xét ΔABC có AD là đường phân giác ứng với cạnh BC(gt)
nên \(\dfrac{BD}{AB}=\dfrac{CD}{AC}\)
hay \(\dfrac{BD}{4}=\dfrac{CD}{3}\)
mà BD+CD=5
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BD}{4}=\dfrac{CD}{3}=\dfrac{BD+CD}{4+3}=\dfrac{5}{7}\)
Do đó: \(BD=\dfrac{20}{7}cm;CD=\dfrac{15}{7}cm\)

a,+)Áp dụng định lí py ta go vào tam giác vuông ABC ta có :
BC=\(\sqrt{AC^2-AB^2}\)
\(\Rightarrow BC=\sqrt{12^2-9^2}\)
\(\Rightarrow BC=3\sqrt{7}\)
+) Áp dụng hệ thức lượng trong tam giác ABC có:
\(BH\times AC=AB\times BC\)
\(\Leftrightarrow BH\times12=9\times3\sqrt{7}\)
\(\Leftrightarrow BH\approx5,95\)
b,Ta có AB=BD(=R)
=>tam giác ABC cân tại A
mà AH là đường cao => AH cũng là tia phân giác BAD hay AC là tia p/g góc BAD
c) xét tam giác ABC và tam giác ADC có :
AB=AD(=R)
góc A1 = góc A2 (do AC là tia p/g)
AC chung
=> tam giác ABC= tam giác ADC (c-g-c)
=> góc B =góc D (=90 độ) => \(AD\perp DC\)=> DC là tiếp tuyến (A:AB)
HÌNH BẠN TỰ VẼ NHÉ!

Hình bạn tự vẽ nha.
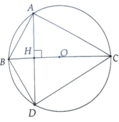
a, \(\Delta ABC\)có: \(OA=OB=OC=\frac{1}{2}BC\Rightarrow\Delta ABC\)vuông tại A
b, \(\left(O;R\right)\)có: \(AD\perp BC=\left\{H\right\}\Rightarrow\)H là trung điểm của AD (liên hệ giữa đường kính và dây)
\(\Delta ACD\)có: CH vừa là đường cao, vừa là đường trung tuyến \(\Rightarrow\Delta ACD\)cân tại C \(\Rightarrow AC=CD\)
Chứng minh tương tự ta có: \(\Delta ABD\)cân tại B có BC là đường cao \(\Rightarrow\)BC là phân giác của \(\widehat{ABD}\)
c, Chứng minh tương tự câu a ta có: \(\Delta BDC\)vuông tại D \(\Rightarrow\widehat{BDA}+\widehat{ADC}=90^o\)(2 góc nhọn phụ nhau) (1)
\(\Delta ABH\)có: \(\widehat{AHB}=90^o\Rightarrow\widehat{ABH}+\widehat{HAB}=90^o\)( 2 góc nhọn phụ nhau)
mà \(\widehat{DAB}=\widehat{BDA}\)(\(\Delta ABD\)cân tại B)
\(\Rightarrow\widehat{ABH}+\widehat{BDA}=90^o\)(2)
Từ (1), (2) \(\Rightarrow\widehat{ABH}=\widehat{ADC}\Leftrightarrow\widehat{ABC}=\widehat{ADC}\)

a) Có AH2=HF.HD \(\rightarrow\)\(\frac{AH}{HF}=\frac{HD}{AH}\)
Xét \(\Delta\)AHD và \(\Delta\)FHA có:
\(\widehat{AHD}=\widehat{FHA}=90^o\)
\(\frac{AH}{HF}=\frac{HD}{AH}\)( chứng minh trên)
\(\rightarrow\Delta\)AHD\(\approx\)\(\Delta\)FHA (c-g-c)
\(\rightarrow\)\(\widehat{ADH}=\widehat{FAH}\)( 2 góc tương ứng)
mà \(\widehat{ADH}+\widehat{HAD}=90^o\)
nên \(\widehat{FAH}+\widehat{HAD}=90^o\)
hay \(\widehat{FAD}=90^o\)\(\rightarrow\Delta\)ADF vuông tại A

45 C B A D M N O 45 O X a b x
Từ D, kẻ DM, DN vuông góc CA và CB.
Khi đo ta dễ thấy DMCN là hình vuông. Vậy thì đặt DM = MC = CN = ND = x.
Áp dụng định lý Talet ta có:
\(\frac{DM}{BC}=\frac{MA}{AC}\Rightarrow\frac{x}{a}=\frac{b-x}{b}\Rightarrow xb=ab-xa\Rightarrow x\left(a+b\right)=ab\)
\(\Rightarrow x=\frac{ab}{a+b}\).
Lại có \(CD=x\sqrt{2}=\frac{ab}{\left(a+b\right)sin45^o}.\)
Cô nghĩ như thế này mới đúng.
Trên tia đối tia CB lấy điểm P sao cho \(CP=CB=b\). Khi đó dễ thấy \(BP=BC+CP=a+b\) . Để ý rằng \(\Delta ACP\) vuông cân tại C nên \(AP=PC\sqrt{2}=b\sqrt{2}\)
Hơn nữa, do CD là tia phân giác của góc BCA vuông nên \(\widehat{BCD}=45^o\), từ đó suy ra CD//AP do có 2 góc đồng vị là \(\widehat{P}\) và \(\widehat{BCD}\) bằng nhau (vì chúng cùng bằng \(45^o\))
Trong tam giác ABP có CD//AP nên \(\dfrac{CD}{AP}=\dfrac{BC}{BP}\) hay \(CD=\dfrac{AP.BC}{BP}=\dfrac{b\sqrt{2}.a}{a+b}=\dfrac{ab}{\left(a+b\right).\dfrac{1}{\sqrt{2}}}=\dfrac{ab}{\left(a+b\right).sin45^o}\) (đpcm)
gọi E, F lần lượt là chân đường vuông góc hạ từ D xuống AC, CB.
tứ giác DECF có 3 góc vuông và CD là phân giác góc \(\widehat{ECF}\)
=> DECF là hình vuông
gọi x (đvđd) là cạnh hình vuông DECF, CD là đường chéo hình vuông => CD = \(x\sqrt{2}\) (đvđd)
theo Talet: \(\dfrac{BF}{BC}=\dfrac{DF}{AC}\)hay \(\dfrac{a-x}{a}=\dfrac{x}{b}\Rightarrow ba-bx=ax\Rightarrow ab=x\left(a+b\right)\Rightarrow x=\dfrac{ab}{a+b}\)=> \(CD=x\sqrt{2}=\dfrac{ab}{a+b}\sqrt{2}=\dfrac{ab}{\left(a+b\right).\sin45^o}\) (đpcm)