Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét ΔABH và ΔCAH có:
\(\widehat{AHB}=\widehat{CHA}=90\left(gt\right)\)
\(\widehat{ABH}=\widehat{CAH}\) (cùng phụ với \(\widehat{BAH}\) )
=>ΔABH=ΔCAH (g.g)
=>\(\frac{AB}{AC}=\frac{AH}{CH}=\frac{BH}{AH}\)
=>\(\frac{20}{21}=\frac{420}{HC}=\frac{BH}{420}\)
=>\(HC=\frac{420\cdot21}{20}=441\)
\(BH=\frac{420\cdot20}{21}=400\)
=> BC=HC+HB=441+400=841
Áp dụng hệ thức giữa cạnh góc vuông và hình chiếu của nó trên cạnh huyền ta có:
\(AB^2=BH\cdot BC=400\cdot841=336400\Rightarrow AB=580\)
\(AC^2=HC\cdot BC=441\cdot841=370881\Rightarrow AC=609\)
Vậy chu vi của ΔABC là: AB+AC+BC=580+609+841=2030

Giải:
Ta có: AB:AC = 20 : 21
=> AB:20 = AC:21 (1)
Đặt tỉ số (1) = X,ta có : AB =20X ; AC=21X
Áp dụng định lí PY-TA-GO,ta có:
BC=√(AB2+AC2)=√(20X)2+(21X)2=√(400X2+441X2)=√881X2=29X
Áp dụng hệ thức cạnh và đường cao trong tam giác ABC vuông tại A,ta có:
AH = (ABxAC):BC =(20X x 21X):29X =(140:3) X
=> 420 = (140:3)X => X = 9
=> AB = 20 x 9 = 180 (cm)
=> AC = 21 x 9 = 189 (cm)
=> BC = 29 x 9 =261 (cm)
=> Pabc = 180 + 189 + 261= 630 (cm)

AB/AC = 20/21 => Đặt AB/20 = AC / 21 = x
=> AB = 20x ; AC= 21x
Tam giác ABC vuông tại A , theo PY TA GO :
\(BC=\sqrt{AB^2+AC^2}=\sqrt{\left(20x\right)^2+\left(21x\right)^2}=\sqrt{400x^2+441x^2}=\sqrt{881x^2}=29x\)
Tam giác ABC vuông tại A, theo HTL :
AH = \(\frac{AB.AC}{BC}=\frac{20x.21x}{29x}=\frac{140}{3}x\)
=> 420 = 140/3 * x => x = 9
=> AB = 20 . 9 = 180
=> AC = 21.9 = 189
=> BC = 29 . 9 =261
=> Cabc = 180 + 189 + 261= 630

\(\dfrac{AB}{AC}=\dfrac{20}{21}\Rightarrow AB=\dfrac{20AC}{21}\)
Áp dụng hệ thức lượng:
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\Leftrightarrow\dfrac{1}{420^2}=\dfrac{1}{\left(\dfrac{20}{21}AC\right)^2}+\dfrac{1}{AC^2}=\dfrac{841}{400AC^2}\)
\(\Rightarrow AC=609\) \(\Rightarrow AB=\dfrac{20}{21}AC=580\)
\(BC=\sqrt{AB^2+AC^2}=841\)
Chu vị: \(609+580+841=2030\)


Lap mình hỏng rồi nên mình chụp lên, bạn chịu khó nhìn nha!!!
Chúc bạn học thật tốt!:))

Tam giac ABC đồng dạng tam giác HAC (cùng vuông và có chung góc C)
AB/AC = AH/HC = 20/21
HC = 21AH/20 = 441
==> AC = căn(AH^2 + HC^2) =căn(420^2 + 441^2) = 609
AB/AC = 20/21
AB = 20/21*609 = 580
BC = căn(AB^2 + AC^2) = căn(580^2 + 609^2) = 841
Chu vi tam giác ABC = tổng 3 cạnh
C = AB + AC + BC = 580 + 609 + 841 = 2030

1.
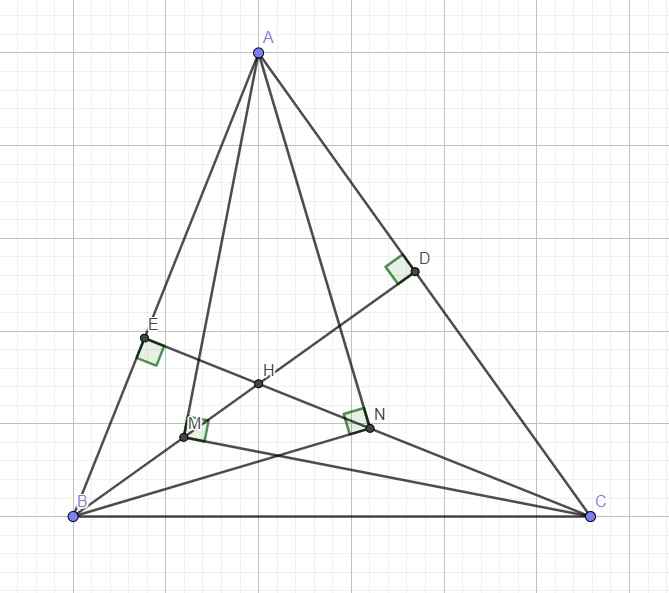
Tam giác AMC vuông tại M với đường cao MD
Áp dụng hệ thức lượng: \(AM^2=AD.AC\) (1)
Tương tự ta có:
\(AN^2=AE.AB\) (2)
Mặt khác xét hai tam giác vuông ABD và ACE có:
\(\widehat{BAC}\) chung
\(\Rightarrow\Delta_VABD\sim\Delta_VACE\) (g.g)
\(\Rightarrow\dfrac{AB}{AC}=\dfrac{AD}{AE}\) \(\Leftrightarrow AB.AE=AC.AD\) (3)
(1);(2);(3) \(\Rightarrow AM^2=AN^2\) \(\Rightarrow AM=AN\)
Bài 2 tham khảo tại đây:
Cho tam giác ABC vuông tại A , đường cao AH . Biết AB/AC = 20/21 , AH = 420 . Tính chu vi tam giác ABC - Hoc24

Có:
\(\dfrac{AB}{AC}=\dfrac{4}{3}=\dfrac{4k}{3k}\) (k là số bất kì)
\(\Rightarrow AB=4k,AC=3k\)
Áp dụng đl pytago vào tam giác ABC được:
\(BC^2=AB^2+AC^2=\left(4k\right)^2+\left(3k\right)^2=16k^2+9k^2=25k^2=\left(5k\right)^2\\ \Rightarrow BC=5k\left(cm\right)\)
Theo hệ thức lượng, có:
\(AH.BC=AB.AC\\ \Leftrightarrow3,6.5k=4k.3k\\ \Leftrightarrow18=12k\\ \Rightarrow k=\dfrac{18}{12}=\dfrac{3}{2}\)
\(\Rightarrow\left\{{}\begin{matrix}AB=4k=4.\dfrac{3}{2}=6\left(cm\right)\\AC=3k=3.\dfrac{3}{2}=\dfrac{9}{2}=4,5\left(cm\right)\\BC=5k=5.\dfrac{3}{2}=\dfrac{15}{2}=7,5\left(cm\right)\end{matrix}\right.\)
\(\Rightarrow P_{ABC}=AB+AC+BC=6+4,5+7,5=18\left(cm\right)\)

 tham khảo câu tl nàu nhé !
tham khảo câu tl nàu nhé !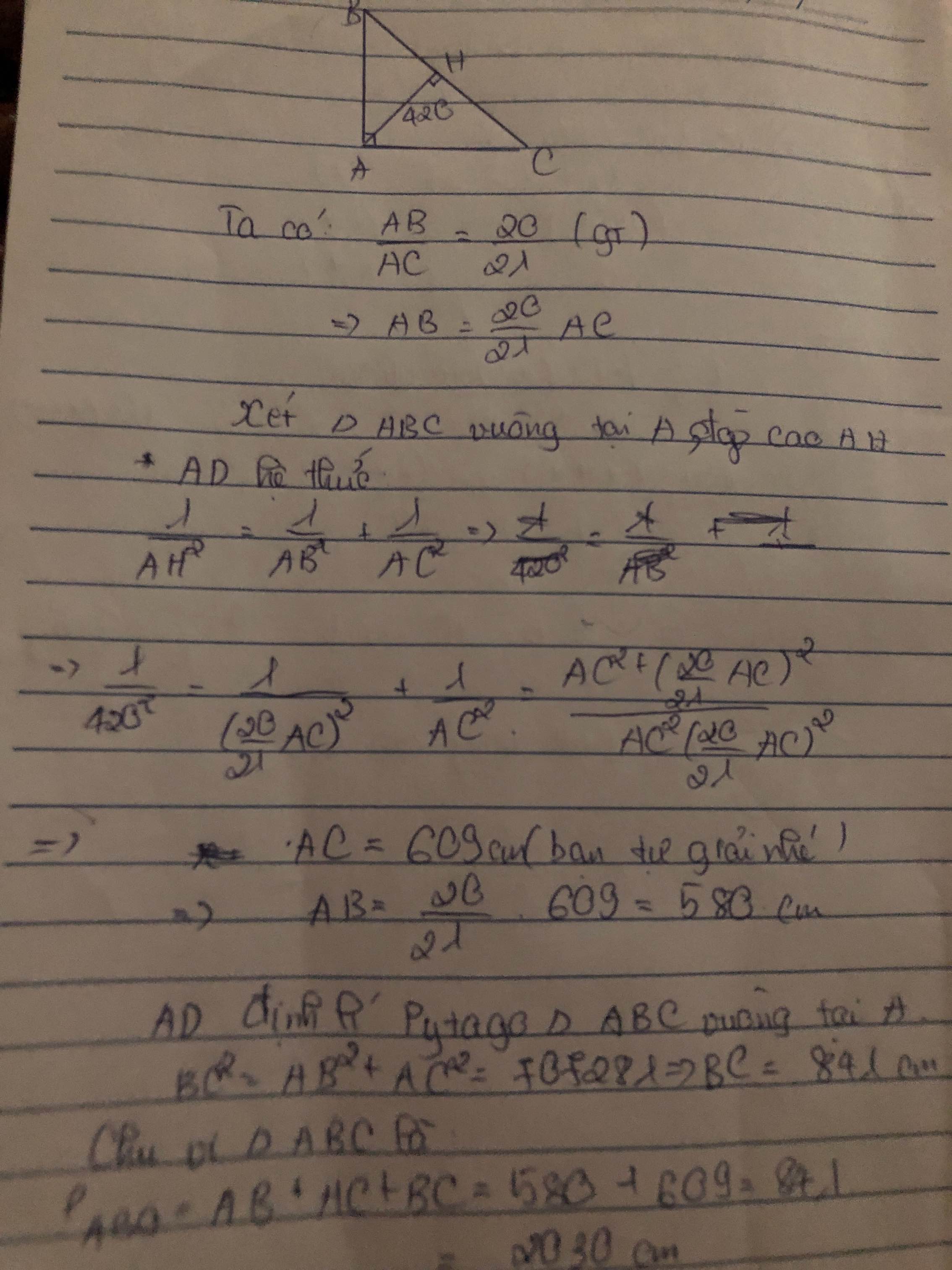

Lôi một bài từ rất lâu rồi ra làm nó không hay lắm nhưng tại thấy không ai trên này làm giống cách mình nên muốn làm thêm cái cách khác thôi:v
Theo đề, ta có: \(\dfrac{AB}{AC}=\dfrac{20}{21}\Rightarrow AB=\dfrac{20AC}{21}\)
Vì ∆ABC vuông tại A nên áp dụng hệ thức lượng, ta có:
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}=\dfrac{1}{420^2}\)
\(\Leftrightarrow\dfrac{1}{\left(\dfrac{20AC}{21}\right)^2}+\dfrac{1}{AC^2}=\dfrac{1}{420^2}\)
\(\Leftrightarrow\dfrac{21^2}{20^2AC^2}+\dfrac{1}{AC^2}=\dfrac{1}{420^2}\)
\(\Leftrightarrow\dfrac{1}{AC^2}\left(\dfrac{21^2}{20^2}+1\right)=\dfrac{1}{420^2}\)
\(\Leftrightarrow\dfrac{1}{AC^2}=\dfrac{1}{420^2}:\left(\dfrac{21^2}{20^2}+1\right)=\dfrac{1}{609^2}\)
\(\Rightarrow AC=609\)
\(\Rightarrow\dfrac{1}{AB^2}+\dfrac{1}{609^2}=\dfrac{1}{420^2}\Leftrightarrow\dfrac{1}{AB^2}=\dfrac{1}{420^2}-\dfrac{1}{609^2}=\dfrac{1}{580^2}\)
\(\Rightarrow AB=580\)
Áp dụng định lý Py-ta-go vào ∆ vuông ABC, ta có:
\(BC^2=AB^2+AC^2=580^2+609^2=841^2\)
\(\Rightarrow BC=841\)
Chu vi ∆ABC là: \(C_{\text{∆}ABC}=AB+BC+AC=580+841+609=2031\)
P/s: Dùng máy tính của bạn nên đánh máy lâu vì không quen:")