Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Từ A kẻ đường trung tuyến cắt BC tại D Theo tính chất đường trung tuyến trong tam giác vuông => AD=1/2 BC. Do đó:Tam giác ABC cân tại D Có góc B= 90 - góc C=90-30=60 độ. Nên tam giác ABC đều => BC=2AB Theo t/c tia phân giác ta có: AB/BC=AD/DC=AB/2AB=AD/DC=1/2. Vây tỉ số AD/DC=1/2 Câu b có AB=12,5 tính được BC= 12,5*2=25. Áp dụng Py-ta-go=>AC=21,65. Tính chu vi diện tích thì tự tính nhé

a) tg ABD vuong tai A có BD = 2AD (vi góc D=60; C=30)
mà CD=BD ( vì tg CDB cân tại C: có C = B = 30)
VẬY tỷ số AD/CD = BD/CD = 1/2
b) tg ABC = 1/2 TG ĐỀU mà AB=12,5 => BC= 12,5.2 = 25cm
AC = BC\(\sqrt{3}\)/2= 15CĂN3
S= 1/2 . AB.AC = 1/2 , 12,5 . 15căn3 = 93,75\(\sqrt{3}\)cm2
chu vi tg là; 15căn3 + 25+12,5
tôi đã hoàn thành nhiệm vụ, thưa ngài

a) Xét ΔABC vuông tại A có \(\widehat{C}=30^0\)(gt)
mà cạnh đối diện với \(\widehat{C}\)
nên \(\dfrac{AB}{BC}=\dfrac{1}{2}\)(Định lí)
Xét ΔABC có BD là đường phân giác ứng với cạnh AC(gt)
nên \(\dfrac{AD}{CD}=\dfrac{AB}{BC}\)(Tính chất tia phân giác của tam giác)
hay \(\dfrac{AD}{CD}=\dfrac{1}{2}\)
b) Ta có: \(BC=2\cdot AB\)(cmt)
nên \(BC=2\cdot12.5=25\left(cm\right)\)
Áp dụng định lí Pytago vào ΔBAC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow AC^2=BC^2-AB^2=25^2-12.5^2=468.75\)
hay \(AC=\dfrac{25\sqrt{3}}{2}cm\)
Diện tích tam giác ABC là:
\(S_{ABC}=\dfrac{AB\cdot AC}{2}=\dfrac{12\cdot\dfrac{25\sqrt{3}}{2}}{2}=\dfrac{150\sqrt{3}}{2}=75\sqrt{3}\left(cm^2\right)\)

a) + Δ ABC vuông tại A, có 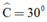
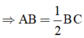
(Trong một tam giác vuông, cạnh đối diện với góc 30o bằng một nửa cạnh huyền)
+ Δ ABC có BD là phân giác của 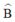
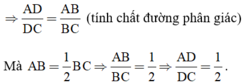
b) AB = 12,5cm ⇒ BC = 2AB = 2.12,5 = 25cm
Áp dụng định lí Py- ta- go vào tam giác ABC ta có:
AB2 + AC2 = BC2 nên AC2 = BC2 - AB2
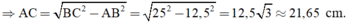
+ Chu vi tam giác ABC là:
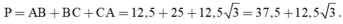
+ Diện tích tam giác ABC là:
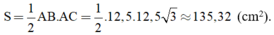

\(\Rightarrow\)AB = 1/2BC ⇒ BC = 2AB
Vì BD là phân giác ⇒ DA/DC = AB/BC = AB/2AB =1/2
b) AB = 12,5 cm \(\Rightarrow\) BC = 25 cm

3:
\(BC=\sqrt{12^2+16^2}=20\left(cm\right)\)
HB=12^2/20=7,2cm
=>HC=20-7,2=12,8cm
\(AD=\dfrac{2\cdot12\cdot16}{12+16}\cdot cos45=\dfrac{48\sqrt{2}}{7}\)
\(HD=\sqrt{AD^2-AH^2}=\dfrac{48}{35}\left(cm\right)\)