Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C O E F S T I Q K D N J L P M G R
a) +) Dễ thấy: ^BAD = ^CAO (Cùng phụ ^ABC). Mà ^BAI = ^CAI nên ^OAI = ^DAI
Suy ra: ^OAI = ^DAO/2 = ^BAI - ^BAD = ^BAC/2 - 900 + ^ABC = ^BAC/2 - (^BAC+^ABC+^ACB)/2 + ^ABC
= (^ABC + ^ACB)/2 = \(\frac{\alpha-\beta}{2}=\frac{\alpha^2-\beta^2}{2\left(\alpha+\beta\right)}=\frac{\alpha^2-\beta^2}{sđ\widebat{BAC}}\) (đpcm).
+) Kẻ đường kính AG của đường tròn (O). Dễ thấy: Tứ giác BICJ nội tiếp, gọi (BICJ) cắt AC tại R khác C.
Do AK=2R nên AK = AG. Ta có: ^ARB = ^ARI + ^BRI = ^IBC + ^ICB = (^ABC+^ACB)/2 = ^ABI + ^IBC = ^ABR
=> \(\Delta\)BAR cân tại A => AB = AR. Kết hợp với AK=AG, ^BAG = ^RAK (cmt) => \(\Delta\)ABG = \(\Delta\)ARK (c.g.c)
=> ^ABG = ^ARK = 900 => ^KRC = ^KDC = 900 => Tứ giác DKCR nội tiếp
=> AD.AK = AR.AC = AI.AJ => Tứ giác DIJK nội tiếp (đpcm).
b) \(\Delta\)KAG cân tại A có phân giác AI => AI vuông góc KG hay AM vuông góc KG. Mà AM vuông góc GM
Nên K,G,M thẳng hàng => K,M,G,N thẳng hàng => AM vuông góc KN tại M
Ta thấy: M là trung điểm IJ, KM vuông góc IJ tại M nên \(\Delta\)KIJ cân tại K
Xét đường tròn (KIJ): KI = KJ, KN vuông góc IJ => KN là đường kính của (KIJ)
Mà D thuộc đường tròn (KIJ) (cmt) => ^KDN = 900 => ND vuông góc AK tại D => N,L,D thẳng hàng
Xét \(\Delta\)AKN có: AM vuông góc KN, ND vuông góc AK, AM và ND cùng đi qua L
=> L là trực tâm \(\Delta\)AKN => KL vuông góc AN (đpcm).
c) Gọi P là trực tâm của \(\Delta\)AJQ
Do \(\Delta\)KIJ cân tại K => ^KIJ = ^KJI. Có tứ giác DIJK nội tiếp => ^KIJ = ^KDJ => ^KDJ = ^KJI
Từ đó: \(\Delta\)DKJ ~ \(\Delta\)JKA (g.g) => KJ2 = KD.KA => KQ2 = KD.KA => \(\Delta\)KQD ~ \(\Delta\)KAQ (c.g.c)
Suy ra: ^QDJ = ^KDQ + ^KDJ = ^AQK + ^AJK = 1800 - ^QAJ = 1800 - ^QPJ => Tứ giác PQDJ nội tiếp
^PDJ = ^PQJ => ^PDK + ^KDJ = ^PDK + ^QJA = ^PQJ => ^PDK = ^PQJ - ^QJA = 900
=> PD vuông góc AD. Mà BC vuông góc AD tại D nên PD trùng BC hay P nằm trên BC (đpcm).
d) Ta thấy: ^ABC > ^ACB (\(\alpha>\beta\)) => ^BAD < ^CAD. Lại có: ^BAI = ^CAI, ^BAD + ^CAD = ^BAI + ^CAI = ^BAC
Suy ra ^BAD < ^BAI => B và I nằm khác khía so với AD => D thuộc [BF]
Hạ IS, IT vuông góc với AC,AB thì F thuộc [DT] => Thứ tự các điểm trên BC là B,D,F,T,C. Do đó: ^IFC = ^DFK < 900
Ta xét thứ tự các điểm trên cạnh AC:
+) A,S,E,C: Vì IS vuông góc AC, theo thứ tự này thì ^IEC > 900. Cũng dễ có: \(\Delta\)IES = \(\Delta\)IFT (Ch.cgv)
=> ^IES = ^IFT < 900 => ^IFT + ^IEC = 1800 => Tứ giác FIEC nội tiếp => ^ECF = ^DIK
Mà ^DIK = ^DJK = ^DAI = \(\frac{\alpha-\beta}{2}\) nên \(\beta=\frac{\alpha-\beta}{2}\Rightarrow\alpha=3\beta\) (*)
+) A,E,S,C: Trong TH này thì ^IEC < 900 => ^IFT + ^IEC < 1800 => ^ECF + ^EIF > 1800
=> ^ECF > ^DIK hay \(\beta>\frac{\alpha-\beta}{2}\Rightarrow\alpha< 3\beta\) (**)
Từ (*) và (**) suy ra: \(\alpha\le3\beta\) (đpcm).

O A B C D E F H K P Q x y S T
a, Xét tứ giác BFEC có ^BFC = ^BEC = 90o
=> Tứ giác BFEC nội tiếp
Xét tứ giác CEHD có ^CEH = ^CDH = 90o
=> tứ giác CEHD nội tiếp
b, Tứ giác BFEC nội tiếp => ^AFE = ^ACB
Mà ^ACB = ^BAx (góc tạo bởi tia tiếp tuyến và dây cung)
=> ^AFE = ^BAx
=> xy // EF (so le trong)
Mà OA _|_ xy (tiếp tuyến)
=> OA _|_ EF
hay OA _|_ PQ
*Vì AQCB nội tiếp
=> ^AQC + ^ABC = 180o (1)
Và ^AEF = ^ABC (2)
Lại có ^AEF + ^AEQ = 180o (3)
Từ (1) ; (2) và (3) => ^AEQ = ^AQC
Còn câu c mình chưa nghĩ ra , có lẽ là chứng minh tứ giác CEPT nội tiếp ...

A B C M O D E F I P Q T
1) Ta có 4 điểm B,O,C,M cùng thuộc đường tròn đường kính OM (^MBO = ^MCO = 900) (1)
Do MI // AB và MB tiếp xúc với (O) tại B nên ^CIM = ^CAB = ^CBM
=> 4 điểm B,I,C,M cùng thuộc một đường tròn (2)
Từ (1) và (2) suy ra 5 điểm M,B,O,I,C cùng thuộc một đường tròn (đpcm).
2) Theo câu a thì M,B,I,C cùng thuộc (OM), có BC giao IM tại F => FI.FM = FB.FC
Đường tròn (O) có dây BC giao DE tại F nên FB.FC = FD.FE
Do vậy FI.FM = FD.FE => \(\frac{FI}{FE}=\frac{FD}{FM}\) (đpcm).
3) Điểm I thuộc đường tròn (OM) => ^OIM = 900 hay ^QIM = 900
Dễ thấy FQ.FT = FB.FC = FI.FM, suy ra tứ giác QMTI nội tiếp => ^QTM = ^QIM = 900
=> \(\Delta\)QTM vuông tại T. Theo ĐL Pytagoras: \(TQ^2+TM^2=QM^2\)
Vậy thì \(\frac{TQ^2+TM^2}{MQ^2}=1.\)

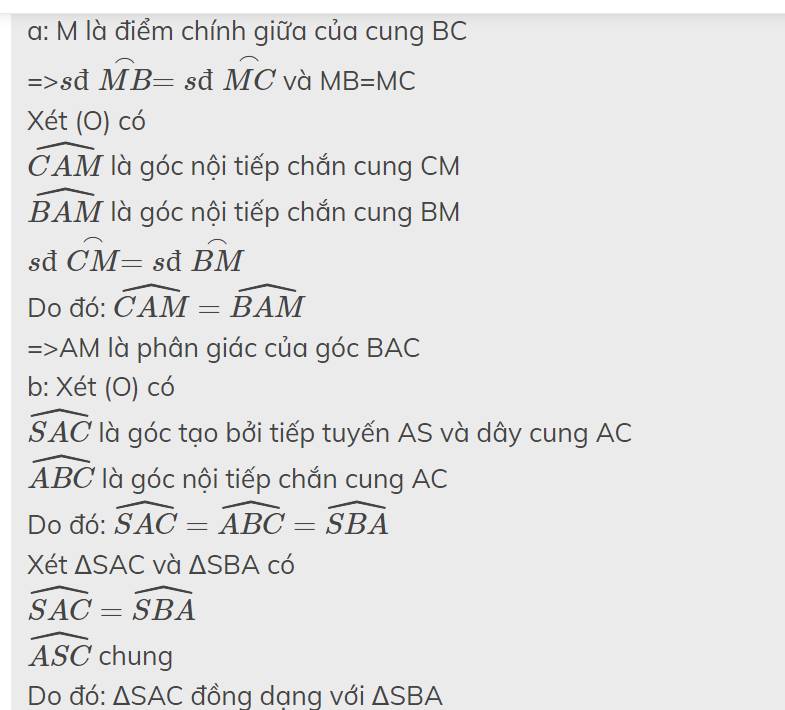


d: \(SA^2=SB\cdot SC\)
\(SE^2=SB\cdot SC\)
=>SA=SE
Xét ΔOAS và ΔOES có
OA=OE
SA=SE
OS chung
Do đó: ΔOAS=ΔOES
=>\(\widehat{OAS}=\widehat{OES}\)
mà \(\widehat{OAS}=90^0\)
nên \(\widehat{OES}=90^0\)
=>E nằm trên đường tròn đường kính SO
mà S,A,O,D cùng thuộc đường tròn đường kính SO(cmt)
nên E nằm trên đường tròn (SAOD)
Ta có ΔOAFΔOAF cân đỉnh O (vì OA=OF=ROA=OF=R)
AH⊥BC→OH⊥AFAH⊥BC→OH⊥AF
OHOH là đường cao của ΔOAFΔOAF cân tại O nên cũn glaf đường trung tuyến
⇒AH=FH⇒AH=FH
Xét ΔAHCΔAHC và ΔEDCΔEDC có:
ˆAHC=ˆEDC=90oAHC^=EDC^=90o
ˆCC^ chung
⇒ΔAHC∼ΔEDC⇒ΔAHC∼ΔEDC (g.g)
⇒AHHC=EDDC⇒AHHC=EDDC
⇒AH.DC=ED.HC⇒AH.DC=ED.HC (do AH=FHAH=FH cmt)
⇒FH.DC=ED.HC