Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Do \(\Delta ABC\) cân tại A \(\Rightarrow\widehat{BCA}=\widehat{CBA}\) hay \(\widehat{BCH}=\widehat{CBA}\)
Xét hai tam giác vuông BHC và CKB có:
\(\left\{{}\begin{matrix}BC\text{ chung}\\\widehat{BCH}=\widehat{CBK}\end{matrix}\right.\) \(\Rightarrow\Delta_VBHC=\Delta_VCKB\left(ch-gn\right)\)
\(\Rightarrow CH=BK\) (1)
Mà \(\Delta ABC\) cân tại A \(\Rightarrow AB=AC\)
\(\Rightarrow AK+BK=AH+CH\) (2)
(1);(2) \(\Rightarrow AK=AH\)
\(\Rightarrow\Delta AHK\) cân tại A

mik cần gấp nha cứu mik
còn bạn nào hcoj giỏi thức ko huhu :((
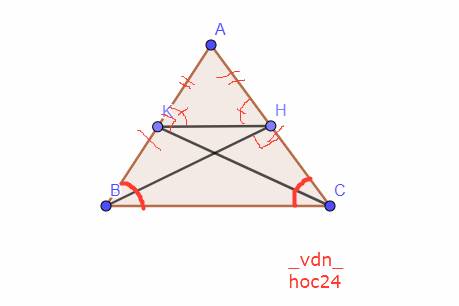
a: Xét ΔABH vuông tại H và ΔACK vuông tại K có
AB=AC
\(\widehat{A}\) chung
Do đó: ΔABH=ΔACK
b: Xét ΔAHK có AH=AK(ΔABH=ΔACK)
nên ΔAHK cân tại A
c: Xét ΔABC có
AK/AB=AH/AC
Do đó: KH//BC

Mình xp sửa đề: Chứng minh: ∆BHA = ∆CKA. Từ đó suy ra ∆AHK cân.
`a,`
Xét Tam giác `BHC` và Tam giác `CKA` có:
\(\widehat{A} \) \(\text{chung}\)
\(AB=AC (\text {Tam giác ABC cân tại A})\)
\(\widehat{AHB}=\widehat{AKC}=90^0\)
`=> \text {Tam giác BHA = Tam giác CKA (ch-gn)}`
`-> AH=AK (\text {2 cạnh tương ứng})`
Xét Tam giác `AHK: AH = AK`
`-> \text {Tam giác AHK cân tại A}`
`b,` Vì Tam giác `AHK` cân tại `A ->`\(\widehat{AKH}=\widehat{AHK}\)
`->`\(\widehat{AHK}=\widehat{AKH}=\)\(\dfrac{180-\widehat{A}}{2}\)
Tam giác `ABC` cân tại `A ->`\(\widehat{ABC}=\widehat{ACB}\)
`->`\(\widehat{ABC}=\widehat{ACB}=\)\(\dfrac{180-\widehat{A}}{2}\)
`->`\(\widehat{AKH}=\widehat{ABC}\)
Mà `2` góc này nằm ở vị trí đồng vị
`-> \text {HK // BC (t/c đt' //)}`

Chẳng hiểu tại sao Mình chẳng thấy gì ở bài làm của cô Chi mà mình vẫn cứ k đúng ???