K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

AH
Akai Haruma
Giáo viên
13 tháng 7 2024
Lời giải:
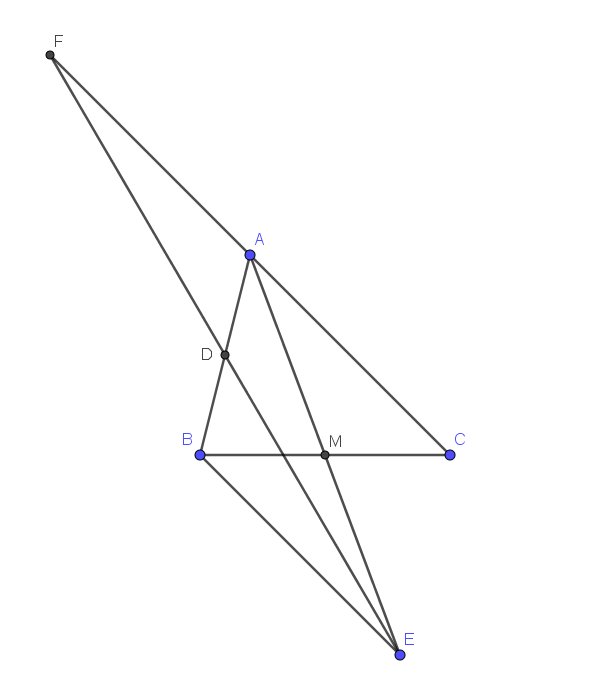
a. Xét tam giác $AMC$ và $EMB$ có:
$AM=ME$
$MB=MC$ (do $M$ là trung điểm $BC$)
$\widehat{AMC}=\widehat{EMB}$ (đối đỉnh)
$\Rightarrow \triangle AMC=\triangle EMB$ (c.g.c)
$\Rightarrow AC=EB$
b. Xét tam giác $AFD$ và $BED$ có:
$FD=ED$
$AD=BD$ (do $D$ là trung điểm $AB$)
$\widehat{ADF}=\widehat{BDE}$ (đối đỉnh)
$\Rightarrow \triangle AFD=\triangle BED$ (c.g.c)
$\Rightarrow AF=BE$
Mà theo phần a thì $AC=BE$ nên $AF=AC$


Bài này khá hay đấy.Mình hướng dẫn bạn nhé.
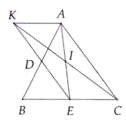
a, tam giác ADK =tam giác BDE (c.g.c) nên AK =BE (2 cạnh tương ứng)
b, Từ 2 tam giác bắng nhau trên suy ra: góc AKD =góc BED ( 2 góc tương ứng)
Mà 2 góc trên ở vị trí so le trong nên AK song song với BE.
c, Bạn nối B với K
Tương tự như ý a và ý b, ta được: tam giác ADE =tam giác BDK(c.g.c) và AE song song với BK
Tam giác ADE =tam giác BDK (cmt) do đó: AE =BK (2 cạnh tứ)
Mặt khác AE =EC (E là trung điểm của AC)
AE song song với KB (cmt) nên góc KBE =góc CEB (so le trong)
Xét tam giác KBE và tam giác CEB có:
BK =CE (=AE)
góc KBE =góc CEB (cmt)
BE là cạnh chung
Do đó: Tam giác KBE =Tam giác CEB (c.g.c)
Suy ra: góc KBE =góc CEB (2 góc tương ứng)
Vậy DE song song với BC (vì có 2 góc so le trong bằng nhau)
Chúc bạn học tốt.
pham van hung a phai xet tam giac truoc chu neu ko thi dua vao dau ma chung minh hai tam giac bang truong hop c.g.c