Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Em tham khảo tại đây nhé.
Câu hỏi của ngdinhthaihoang123 - Toán lớp 7 - Học toán với OnlineMath

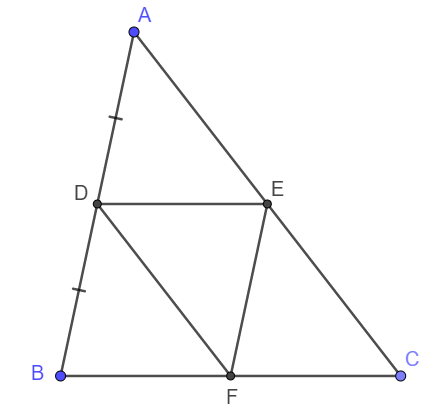
a) Xét tam giác DEF và tam giác FBD có:
Cạnh DF chung
\(\widehat{EDF}=\widehat{BFD}\) (Hai góc so le trong)
\(\widehat{EFD}=\widehat{BDF}\) (Hai góc so le trong)
\(\Rightarrow\Delta DEF=\Delta FBD\left(g-c-g\right)\Rightarrow EF=BD=AD\)
b)
Xét tam giác ADE và tam giác EFC có:
\(\widehat{DAE}=\widehat{FEC}\) (Hai góc so le trong)
\(\widehat{EFC}=\widehat{ADE}\left(=\widehat{DBF}\right)\)
\(\Rightarrow\Delta ADE=\Delta EFC\left(g-c-g\right)\Rightarrow AE=EC\)
Từ đó ta cũng suy ra DE = FC
Lại có do \(\Delta DEF=\Delta FBD\Rightarrow DE=FB\)
Vậy nên FC = FB
c) Ta có FC = FB = DE nên \(DE=\frac{BC}{2}\)
EF = AD = DB nên \(EF=\frac{AB}{2}\)

A B C D E F
* Xét tam giác BDE và tam giác EFB có:
+) \widehat{DEB} = \widehat{EBF} ( so le trong)
+) BE chung
+) \widehat{FEB} = \widehat{DBE} ( so le trong)
=> Tam giác BDE = tam giác EFB ( g.c.g )
=> EF = BD ( 2 cạnh tương ứng)
* Mà AD = BD ( D là trung điểm của AB)
=> EF = AD. ( cpcm)

Bạn tự vẽ hình nha!!!
a) Vì AD // FE nên \(\widehat{ADE}=\widehat{FED}\) (2 góc so le trong) và \(\widehat{AED}=\widehat{FDE}\) (2 góc so le trong)
Xét \(\Delta ADE\) và \(\Delta FED\) có:
\(\widehat{ADE}=\widehat{FED}\) (c/m trên)
DE là cạnh chung
\(\widehat{AED}=\widehat{FDE}\) (c/m trên)
=> \(\Delta ADE=\Delta FED\) (g.c.g)
=> AD=EF (2 cạnh tương ứng)
b) Vì FD // EC nên \(\widehat{DFE}=\widehat{CEF}\) (2 góc so le trong)
Mặt khác DE // CF nên \(\widehat{DEF}=\widehat{CFE}\) (2 góc so le trong)
Xét \(\Delta FED\) và \(\Delta EFC\) có:
\(\widehat{DEF}=\widehat{CFE}\) (c/m trên)
EF là cạnh chung
\(\widehat{DFE}=\widehat{CEF}\) (c/m trên)
=> \(\Delta FED=\Delta EFC\left(g.c.g\right)\)
=> \(\Delta ADE=\Delta EFC\left(\Delta ADE=\Delta FED\right)\)
=> AE=EC (2 cạnh tương ứng)
Vì AD=EF(c/m trên). Mà AD=BD (D là trung điểm của AB)
=> BD=EF
Mặt khác \(\Delta FED=\Delta EFC\) (c/m trên)
=> FD=EC (2 cạnh tương ứng)
Ta có: EF // BD nên \(\widehat{BDF}=\widehat{DFE}\) (2 góc so le trong)
Mà \(\widehat{DFE}=\widehat{CEF}\) (c/m trên) => \(\widehat{BDF}=\widehat{CEF}\)
Xét \(\Delta BDF\) và \(\Delta FEC\) có:
\(\widehat{BDF}=\widehat{CEF}\) (c/m trên)
FD=EC (c/m trên)
\(\widehat{BFD}=\widehat{FCE}\) (FD // EC)
=> \(\Delta BDF=\Delta FEC\left(g.c.g\right)\)
=> BF=FC (2 cạnh tương ứng)
c) Vì \(\Delta FED=\Delta EFC\) (c/m trên) => DE=FC (2 cạnh tương ứng). Mà DF=\(\frac{1}{2}BC\) (BF=FC)
=> DE=\(\frac{1}{2}BC\)
Mặt khác EF=AD (c/m trên). Mà AD=\(\frac{1}{2}BC\) (D là trung điểm của AB)
=> EF=\(\frac{1}{2}AB\)

a: Xét tứ giác BDEF có
BD//EF
DE//BF
Do đó: BDEF là hình bình hành
=>EF=BD=AD
b: Xét ΔADE và ΔEFC có
AD=EF
góc ADE=góc EFC
DE=FC
Do đó: ΔADE=ΔEFC
c: Xét ΔABC có
D là trung điểm của AB
DE//BC
Do đó: E là trung điểm của AC
=>EA=EC
d: Xét ΔABC có AD/AB=AE/AC
nên DE//BC và DE=BC/2

DF la canh chung
góc EDF = góc DFB ( 2 góc so le trong của DE//BC)
góc BDF = Góc EDF( 2 góc so le trong của EF//AB)
=> tam giác CEF= tam giác FBD (g.c.g)
=>EF = DB ( 2 cạnh tương ứng)
mà BD= AD ( D la trung diem cua AB)
=> EF= AD(dpm)
- goc BDF + goc FDE + gocEDA=180
- goc BFD + goc DFE+goc EFC=180
mà goc BDF=goc EFD (chứng minh trên: cmt)
goc FDE= goc DBF (cmt)
=> goc EDA= goc EFC
Xét tam giác ADE và tam giác EFC có
EF=AD(cmt))
góc EDA = EFC ( cmt)
góc FEC= góc EAD ( 2 góc đồng vị của EF//AB)
=> tam giác ADE = tam giác EFC ( dpcm)
c, Vi tam giác ADE= tam giác EFC
=> AE=EC( 2 cạnh tương ứng)

Đay lè p!
Câu hỏi của Đỗ Lê Tú Linh - Toán lớp 7 - Học toán với OnlineMath
Câu hỏi của Đỗ Lê Tú Linh - Toán lớp 7 - Học toán với OnlineMath ![]()
![]()
![]()
![]()
