Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải thích các bước giải:
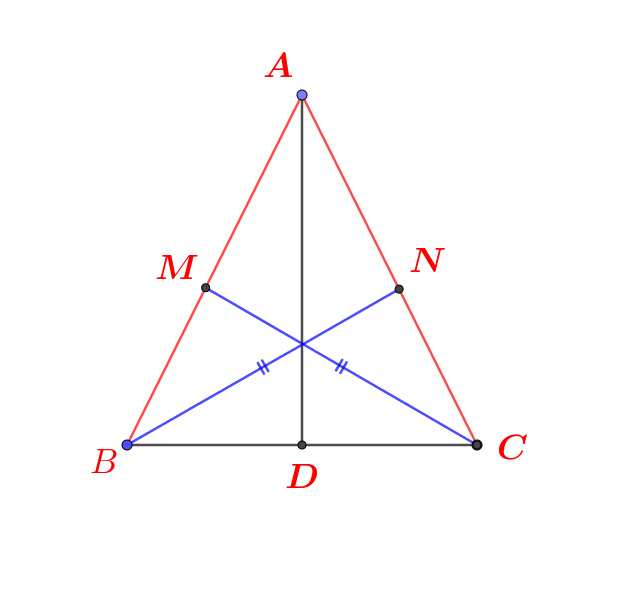
Do G là trọng tâm ΔABC
\(\to \frac{{GC}}{{CE}} = \frac{2}{3};\frac{{BG}}{{BD}} = \frac{2}{3}\)
Mà GM//AB; GN//AC hay GM//BE; GN//DC
Theo định lí ta-lét trong ΔCBE và BDC
\(\begin{array}{l} \to \frac{{GC}}{{CE}} = \frac{{CM}}{{CB}} = \frac{2}{3};\frac{{BG}}{{BD}} = \frac{{BN}}{{BC}} = \frac{2}{3}\\ \to \frac{{CM}}{{BC}} = \frac{{BN}}{{BC}} = \frac{2}{3} \to \frac{{BM}}{{BC}} = \frac{{CN}}{{BC}} = \frac{1}{3}\\ \to CM = BN;BM = CN\\ \to BM = MN = CN \end{array}\)

Bạn tham kháo nha:
https://olm.vn/hoi-dap/detail/8338961574.html

A B C D E M N I K
Dễ chứng minh I là trung điểm BD, K là trung điểm CE.
Ta có tính chất: Trong hình thang, đoạn thẳng nối trung điểm hai đường chéo song song với hai đáy và có độ dài bằng nửa hiệu độ dài hai đáy. (chưa nghĩ ra cách chứng minh)
Do đó xét hình thang BEDC có I và K là trung điểm hai đường chéo nên
\(IK=\frac{BC-ED}{2}=\frac{BC-\frac{1}{2}BC}{2}=\frac{\frac{1}{2}BC}{2}=\frac{1}{4}BC=\frac{a}{4}\)
Từ từ nghĩ cách chứng minh tính chất trên nha!