Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

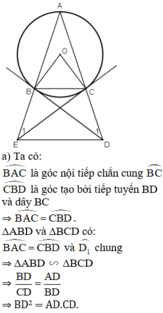
b) ΔABC cân tại A
⇒ AB = AC
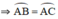
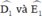 là các góc có đỉnh ở bên ngoài đường tròn nên ta có:
là các góc có đỉnh ở bên ngoài đường tròn nên ta có:
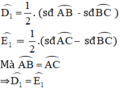
⇒ D và E cùng nhìn BC dưới 1 góc bằng nhau
⇒ BCDE là tứ giác nội tiếp.
c. Tứ giác BCDE nội tiếp

⇒ BC // DE (hai góc đồng vị bằng nhau).

b) ΔABC cân tại A
⇒ AB = AC
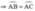
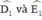 là các góc có đỉnh ở bên ngoài đường tròn nên ta có:
là các góc có đỉnh ở bên ngoài đường tròn nên ta có:
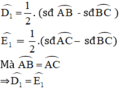
⇒ D và E cùng nhìn BC dưới 1 góc bằng nhau
⇒ BCDE là tứ giác nội tiếp.
c. Tứ giác BCDE nội tiếp

⇒ BC // DE (hai góc đồng vị bằng nhau).

câu c. chứng minh hai góc trong cùng phía bù nhau góc BCD và CDE
Làm câu c) thôi ạ ._.
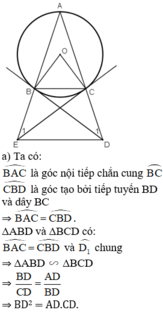
A B C D E 1 1 O
c) Tứ giác BCDE nội tiếp :
\(\Rightarrow\widehat{BED}+\widehat{BCD}=180^o\)
Mà \(\widehat{BCD}+\widehat{ACD}=180^o\)( hai góc kề bù )
\(\Rightarrow\widehat{BED}=\widehat{ACB}\)
Mà \(\widehat{ACB}=\widehat{ABC}\)( \(\Delta ABC\)cân tại A )
\(\Rightarrow\widehat{BED}=\widehat{ABC}\)
=> BC // DE ( hai góc đồng vị bằng nhau )

a) Xét ΔADB∆ADB và ΔBDC∆BDC, ta có:
ˆBAD=ˆCBDBAD^=CBD^ (góc nội tiếp cùng chắn cung BCBC)
ˆD1D1^ góc chung
Vậy ΔADB∆ADB đồng dạng ΔBDC∆BDC ⇒ BDCD=ADBD=BD2=AD.CDBDCD=ADBD=BD2=AD.CD (đpcm)
b) Ta có ˆAECAEC^ là góc có đỉnh ở bên ngoài (O)(O)
Quảng cáo
ˆAEC=sđAC−sđBC2=sđAB−sđBC2=ˆADBAEC^=sđAC⏜−sđBC⏜2=sđAB⏜−sđBC⏜2=ADB^
Xét tứ giác BCDEBCDE, ta có: ˆAECAEC^ và ˆADBADB^ là hai góc liên tiếp cùng nhìn đoạn BCBC và ˆAEC=ˆADBAEC^=ADB^ . Vậy tứ giác BCDEBCDE nội tiếp đường tròn
c) Ta có: ˆACB+ˆBCD=1800ACB^+BCD^=1800 (hai góc kề bù).
hay ˆABC+ˆBCD=1800ABC^+BCD^=1800 (ΔABC∆ABC cân tại AA)
⇒ˆABC=1800–ˆBCD(1)⇒ABC^=1800–BCD^(1)
Vì BCDEBCDE là tứ giác nội tiếp nên
ˆBED+ˆBCD=1800⇒ˆBED=1800–ˆBCD(2)BED^+BCD^=1800⇒BED^=1800–BCD^(2)
So sánh (1) và (2), ta có: ˆABC=ˆBEDABC^=BED^
Ta cũng có: ˆABCABC^ và ˆBEDBED^ là hai góc đồng vị. Suy ra: BC//DEBC//DE (đpcm)
a) Xét ΔADB∆ADB và ΔBDC∆BDC, ta có:
ˆBAD=ˆCBDBAD^=CBD^ (góc nội tiếp cùng chắn cung BCBC)
ˆD1D1^ góc chung
Vậy ΔADB∆ADB đồng dạng ΔBDC∆BDC ⇒ BDCD=ADBD=BD2=AD.CDBDCD=ADBD=BD2=AD.CD (đpcm)
b) Ta có ˆAECAEC^ là góc có đỉnh ở bên ngoài (O)(O)
Quảng cáo
ˆAEC=sđAC−sđBC2=sđAB−sđBC2=ˆADBAEC^=sđAC⏜−sđBC⏜2=sđAB⏜−sđBC⏜2=ADB^
Xét tứ giác BCDEBCDE, ta có: ˆAECAEC^ và ˆADBADB^ là hai góc liên tiếp cùng nhìn đoạn BCBC và ˆAEC=ˆADBAEC^=ADB^ . Vậy tứ giác BCDEBCDE nội tiếp đường tròn
c) Ta có: ˆACB+ˆBCD=1800ACB^+BCD^=1800 (hai góc kề bù).
hay ˆABC+ˆBCD=1800ABC^+BCD^=1800 (ΔABC∆ABC cân tại AA)
⇒ˆABC=1800–ˆBCD(1)⇒ABC^=1800–BCD^(1)
Vì BCDEBCDE là tứ giác nội tiếp nên
ˆBED+ˆBCD=1800⇒ˆBED=1800–ˆBCD(2)BED^+BCD^=1800⇒BED^=1800–BCD^(2)
So sánh (1) và (2), ta có: ˆABC=ˆBEDABC^=BED^
Ta cũng có: ˆABCABC^ và ˆBEDBED^ là hai góc đồng vị. Suy ra: BC//DEBC//DE (đpcm)

a) Xét (O) có
\(\widehat{BAC}\) là góc nội tiếp chắn cung BC
\(\widehat{DBC}\) là góc tạo bởi dây cung BC và tiếp tuyến BD
Do đó: \(\widehat{BAC}=\widehat{DBC}\)(Hệ quả góc tạo bởi tiếp tuyến và dây cung)

a: Xét tứ giác BCDE có
\(\widehat{BEC}=\widehat{BDC}=90^0\)
Do đó:BCDE là tứ giác nội tiếp
b: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
\(\widehat{A}\) chung
Do đó: ΔADB\(\sim\)ΔAEC
Suy ra: \(\dfrac{AD}{AE}=\dfrac{AB}{AC}=\dfrac{2\cdot AM}{2\cdot AN}=\dfrac{AM}{AN}\)
hay \(AE\cdot AM=AN\cdot AD\)