Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Kẻ DE//AB. BD/CD = AE/EC = AB/AC => AE/(EC+AE) = AB/(AB+AC) <=> AE = 10
^BAD = ^ADE (so le trong) => T/g ADE cân tại E
Kẻ EH vuông góc với AD => AH = 1/2 AD = 6. Theo đ/l Py-ta-go tính được EH = 8
=> S(ADE) = 48
S(ADE)/S(ADC) = AE/AC = 5/7 => S(ADC) = 67,2
S(ABD)/S(ADC) = BD/CD = 35/14 = 5/2 => S(ABD) = 168
=> S(ABC) = 235,2 (cm^2)

Kẻ DE//AB. BD/CD = AE/EC = AB/AC => AE/(EC+AE) = AB/(AB+AC) <=> AE = 10
^BAD = ^ADE (so le trong) => T/g ADE cân tại E
Kẻ EH vuông góc với AD => AH = 1/2 AD = 6. Theo đ/l Py-ta-go tính được EH = 8
=> S(ADE) = 48
S(ADE)/S(ADC) = AE/AC = 5/7 => S(ADC) = 67,2
S(ABD)/S(ADC) = BD/CD = 35/14 = 5/2 => S(ABD) = 168
=> S(ABC) = 235,2 (cm^2)

vẽ: DE//AB, ta có: \(\frac{AE}{EC}=\frac{DB}{BC}=\frac{AB}{AC}\)
thay vào AE/EC ta có: \(\frac{AE}{EC}=\frac{14}{35}\)
đặt AE = x thì EC = 35 - x, thay vao đăng thức, ta có:
\(\frac{x}{35-x}=\frac{14}{35}\)
\(\Rightarrow490-14x=35x\)
\(\Rightarrow x=10\)
trong tam giác AED cân tại E vẽ đường cao EH.
=> EH là đường trung tuyến nên AH = 6.
áp dụng ĐL pi-ta-go vào tam giác vuông AHE.
\(\Rightarrow EH=8\text{ nen }S_{\text{tam giác }}ADE=48cm^2\)
do tam giác ADE và DCE có chung đường cao nên SDEC = 120 cm2
\(\Rightarrow\orbr{\begin{cases}S_{ADC}=168cm^2\\S_{ABC}=235,2cm^2\end{cases}}\)

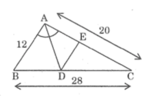
Vì △ ABD và △ ABC có chung đường cao kẻ từ đỉnh A nên:
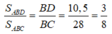
Vậy: S A B D = 3/8.S
S A D C = S A B C - S A B D = S - 3/8.S = 8/8.S - 3/8.S = 5/8.S
Vì DE // AB và AD là đường phân giác góc A nên AE = DE
Ta có: 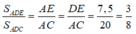
Vậy: 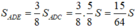
Ta có: 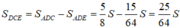

a) Xét tam giác BAD và CAD có:
AB=AC=14cm
\(\widehat{BAD}=\widehat{CAD}\)(AD là tia phân giác)
AD cạnh chung
=> \(\Delta BAD=\Delta CAD\left(c.g.c\right)\)
=> BD=CD
Mà BD+CD=BC=12 cm
=> BD=DC=12:2=6(cm)
b) Vì AB=AC, BD=DC
=> AD là đường trung trực của BC
=> AD _|_ BC
=> \(S_{\Delta ABD}=\frac{1}{2}AD\cdot BD;S_{\Delta CAD}=\frac{1}{2}AD\cdot DC\)
\(\frac{S_{\Delta ABD}}{S_{\Delta CAD}}=\frac{AD\cdot BD}{AD\cdot DC}=\frac{AD}{DC}=1\)