Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

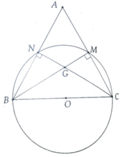
a, Ta có: B N C ^ = 90 0 => N ∈ (O; B C 2 )
B M C ^ = 90 0 => M ∈ (O; B C 2 )
=> B, C, M, N cùng thuộc đường tròn tâm (O; B C 2 )
b, ∆ABC đều có G là trực tâm đồng thời là trọng tâm
∆AOB vuông tại O có R = ON = a 2
Ta có OA = a 2 - a 2 4 = a 3 2 > R
=> A nằm ngoài (O)
Ta có OG = 1 3 OA = a 3 6 < R
=> G nằm ngoài (O)

a: Xét tứ giác BNMC có góc BNC=góc BMC=90 độ
nên BNMC là tứ giác nội tiếp
=>B,N,M,C cùng thuộc (O)
b: Xét (O) có
BC là đường kính
MNlà dây
Do đó: BC>MN
c: Vì ΔABC đều có G là giao của hai đường cao
nên G là tâm đường tròn ngoại tiếp ΔABC và cũng là trọng tâm
=>GA=GC và AG=2/3AO
=>GC>GO
=>G nằm trong (O)

a: góc BMC+góc BNC=90+90=180 độ
=>BMCN nội tiếp
b: Xét ΔAFM và ΔAMK có
góc AMF=góc AKM
góc FAM chung
=>ΔAFM đồng dạng với ΔAMK
=>AF/AM=AM/AK
=>AM^2=AF*AK

b: Xét tứ giác ANHM có
\(\widehat{ANH}+\widehat{AMH}=180^0\)
Do đó: ANHM là tứ giác nội tiếp
hay A,N,H,M cùng thuộc 1 đường tròn

Chúc bạn học tốt nha!!!
chúc bạn học giỏi