Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

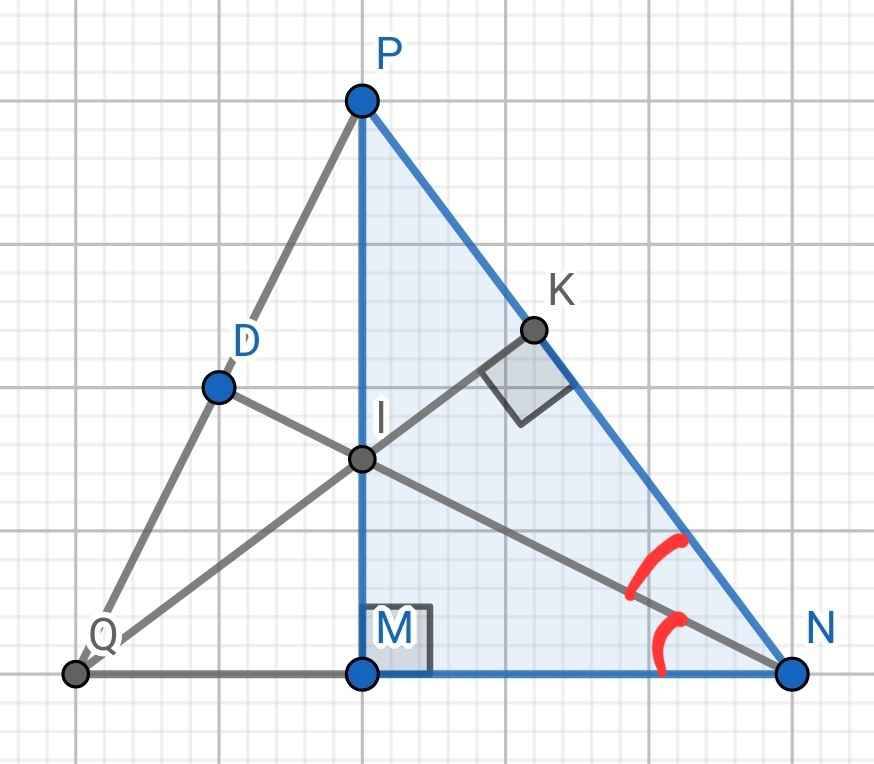
a) Xét hai tam giác vuông: ∆IMN và ∆IKN có:
IN chung
MNI = KNI (do NI là phân giác của ∠MNP)
⇒ ∆IMN = ∆IKN (cạnh huyền - góc nhọn)
b) ∆IKP vuông tại K
IP là cạnh huyền nên IP lớn nhất
IK < IP (1)
Do ∆IMN = ∆IKN (cmt)
⇒ MI = IK (2)
Từ (1) và (2)⇒ MI < IP
c) Xét hai tam giác vuông: ∆IKP và ∆IMQ có:
IM = IK (cmt)
∠PIK = ∠MIQ (đối đỉnh)
∆IKP = ∆IMQ (cạnh góc vuông - góc nhọn kề)
⇒ KP = MQ (hai cạnh tương ứng) (3)
Do ∆IMN = ∆IKN (cmt)
⇒ MN = KN (hai cạnh tương ứng) (4)
Từ (3) và (4) ⇒ KN + KP = MN + MQ
NP = NQ
⇒ ∆NPQ cân tại N
Lại có NI là phân giác của ∠MNP
⇒ NI là phân giác của ∠QNP
⇒ NI cũng là đường cao của ∆NPQ (tính chất tam giác cân)
⇒ ND ⊥ QP

a: Xét ΔNMI vuông tại M và ΔNKI vuông tại K co
NI chung
góc MNI=góc KNI
=>ΔNMI=ΔNKI
b: Xet ΔIMA vuông tại M và ΔIKP vuông tại K có
IM=IK
góc MIA=góc KIP
=>ΔIMA=ΔIKP
=>KI=IM
=>KI<IA

1: Xét ΔNMI và ΔNEI co
NM=NE
góc MNI=góc ENI
NI chung
=>ΔNMI=ΔNEI
=>IM=IE
=>ΔIME cân tại I
2: góc KME+góc NEM=90 độ
góc PME+góc NME=90 độ
mà góc NEM=góc NME
nên góc KME=góc PME
=>ME là phân giác của góc KMP
3: góc MIQ=90 độ-góc MNI
góc MQI=góc NQK=90 độ-góc PNI
mà góc MNI=góc PNI
nên góc MIQ=góc MQI
=>ΔMIQ cân tại M
4: Xét ΔIMF vuông tại M và ΔIEP vuông tại E có
IM=IE
góc MIF=góc EIP
=>ΔIMF=ΔIEP
=>MF=EP
Xét ΔNFP có NM/MF=NE/EP
nên ME//FP

a)
Xét tam giác NMD và tam giác NED, có:
NM=EH(gt)
\(\widehat{MND}=\widehat{DNE}\)(do MD là phân giác MNE)
ND là cạnh chung
Suy ra: Tam giác NMD=tam giác NED (c.g.c)
==> \(\widehat{NMD}=\widehat{NED}\) (2 góc tương ứng)
b) Có: +) MN vuông góc MP
+) EH vuông góc MP
==> MN // EH
c) Có : MN // EH
==> MNP = HEP (2 góc đồng vị)

1: Xét ΔNMI vuông tại M và ΔNKI vuông tại K có
NI chung
\(\widehat{MNI}=\widehat{KNI}\)
Do đó: ΔNMI=ΔNKI
Suy ra: NM=NK
hay ΔNMK cân tại N
2: Xét ΔMIQ vuông tại M và ΔKIP vuông tại K có
IM=IK
\(\widehat{MIQ}=\widehat{KIP}\)
Do đó: ΔMIQ=ΔKIP
Suy ra: MQ=KP
Ta có: NM+MQ=NQ
NK+KP=NP
mà NM=NK
và MQ=KP
nên NQ=NP
hayΔNQP cân tại N
3: Xét ΔNQP có
NM/MQ=NK/KP
nên MK//QP


a: Xet ΔIMN và ΔIKN có
NM=NK
góc MNI=góc KNI
NI chung
=>ΔIMN=ΔIKN
=>góc IKN=90 độ
b:Xet ΔNKA vuông tại K và ΔNMP vuông tại M có
NK=NM
góc N chung
=>ΔNKA=ΔNMP
=>NA=NP
=>ΔNAP cân tại N
mà NI là phân giác
nên NI vuông góc PA