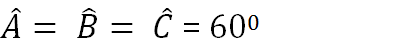DD
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
BM
1
N
9 tháng 11 2018
TH1: m+n+p khác 0
\(\frac{m+n-p}{p}=\frac{n+p-m}{m}=\frac{p+m-n}{n}\)
\(\Rightarrow2+\frac{m+n-p}{p}=2+\frac{n+p-m}{m}=2+\frac{p+m-n}{n}\)
\(\Rightarrow\frac{m+n+p}{p}=\frac{n+p+m}{m}=\frac{p+m+n}{n}\)
\(\Rightarrow p=m=n\)
thay m=n=p vào biểu thức H ta có:
\(H=\left(1+\frac{m}{m}\right).\left(1+\frac{n}{n}\right).\left(1+\frac{p}{p}\right)\)
\(H=2.2.2=2^3=8\)
TH2: m+n+p = 0 (m,n,p khác 0)
=> m=-(n+p)
=> n=-(m+p)
=>p=-(n+m)
thay m=-(n+p), n=-(m+p), p=-(n+m) vào biểu thức H
\(H=\left(1+\frac{-m-p}{m}\right).\left(1+\frac{-n-m}{n}\right).\left(1+\frac{-n-p}{p}\right)\)
\(H=\left(-\frac{p}{m}\right).\left(-\frac{m}{n}\right).\left(\frac{-n}{p}\right)=-1\)
BM
1
17 tháng 6 2022
a: Xét ΔAEC có \(\widehat{AEC}>90^0\)
nên AC là cạnh lớn nhất
=>AC>AE
hay AB>AE
b: Lấy F sao cho M là trung điểm của AF
Xét tứ giác ABFE có
M là trung điểm của FA
M là trung điểm của BE
Do đó: ABFE là hình bình hành
Suy ra: AB=FE và AB//FE
=>FE>AE
=>\(\widehat{EAF}>\widehat{EFA}\)
hay \(\widehat{EAF}>\widehat{BAM}\)(ĐPCM)
11 tháng 11 2017
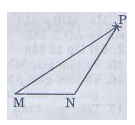
bài 15 :
- Vẽ đoạn thẳng MN = 2,5cm.
- Trên cùng một nửa mặt phẳng bờ MN vẽ cung tròn tâm M bán kính 5cm, và cung tròn tâm N bán kính 3cm
- Hai cung tròn cắt nhau tại P. Vẽ các đoạn thẳng MP, NP ta được tam giác MNP.
11 tháng 11 2017
bài 16 :
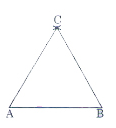
Vẽ tam giác ABC (tương tự với cách vẽ ở Bài 15):
- Vẽ cạnh AB có độ dài bằng 3 cm.
- Trên một nửa mặt phẳng bờ AB lần lượt vẽ hai cung tròn tại A và B có bán kính 3 cm
- Hai cung tròn này cắt nhau tại C. Nối các điểm A, B, C ta được tam giác ABC cần vẽ.
Đo mỗi góc của tam giác ABC ta được:
9 tháng 5 2017
A B C E M I K H
a) Xét \(\Delta AMC\) và \(\Delta EMB\) ,có :
AM = ME ( gt )
MC = MB ( M là trung điểm của BC )
\(\widehat{AMC}=\widehat{EMB}\) ( 2 góc đối đỉnh )
=> \(\Delta AMC=\Delta EMB\left(c.g.c\right)\)
=> \(\left\{{}\begin{matrix}AC=EB\\\widehat{MBE}=\widehat{MCA}\end{matrix}\right.\)
Mà \(\widehat{MBE}\) và \(\widehat{MCA}\) là 2 góc so le trong
=> AC // EB
b) Ta có :
AC // EB
=> \(\widehat{CAM}=\widehat{MEB}\) ( 2 góc so le trong )
Xét \(\Delta AMI\) và \(\Delta EMK\) ,có :
AI = EK (gt )
AM = EM (gt)
\(\widehat{CAM}=\widehat{MEB}\) ( c/m t)
=> \(\Delta AMI=\Delta EMK\left(c.g.c\right)\)
=> \(\widehat{AMI}=\widehat{EMK}\)
Mà \(\widehat{AMI}\) và \(\widehat{EMK}\) là 2 góc ở vị trí đối đỉnh
=> Ba điểm I , M , K thẳng hàng
c) KO có đề bài
7 tháng 12 2022
a: Không có điểm nào trong góc phần tư thứ III
b: Tọa độ điểm E là:
x=0và y-3=0
=>x=0và y=3
Tọa độ F là:
x+3=0 và y=0
=>F(-3;0)
Tọa độ H là:
x-5=0 và 2y+6=0
=>x=5 và y=-3
Tọa độ G là:
x-1=0 và y+5=0
=>x=1 và y=-5