Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) ΔADI và ΔCDL có: góc A = góc C = 90°
AD = CD (hai cạnh hình vuông)
góc D1 = góc D2
cùng phụ với góc CDI
Do đó ΔADI = ΔCDL (g.c.g)
Suy ra DI = DL. Vậy ΔDIL cân
b) Áp dụng hệ thức  là không đổi.
là không đổi.
Nhận xét: Câu a) chỉ là gợi ý để làm câu b). Điều phải chứng minh ở câu b) rất gần với hệ thức 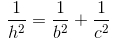
Nếu đề bài không cho vẽ DL ⊥ DK thì ta vẫn phải vẽ đường phụ DL ⊥ DK để có thể vận dụng hệ thức trên.

Hình bạn tự vẽ nha.
a, ABCD là hình vuông \(\Rightarrow AB=BC=CD=AD\)
Ta có: \(\hat{IAD}+\hat{DAE}=90^o\)
\(\hat{BAE}+\hat{DAE}=90^o\)
\(\Rightarrow \hat{IAD} =\hat{BAE}\)
Xét \(\Delta ADI\) và \(\Delta ABE\) có:
\(\hat{ADI}=\hat{ABE}=90^o\)
\(AD=AB\left(cmt\right)\)
\(\hat{IAD}=\hat{BAE}(cmt)\)
\(\Rightarrow\Delta ADI=\Delta ABE\left(g-c-g\right)\Rightarrow AI=AE\)
b, \(\Delta AIK\) có: \(\hat{IAK}=90^o\), \(AD\perp IK\)
\(\Rightarrow AD.IK=AI.AK\) (hệ thức lượng trong tam giác vuông) mà \(AI=AE\left(cmt\right)\Rightarrow AD.IK=AE.AK\)
c, \(\Delta AIK\) có: \(\hat{IAK}=90^o\), \(AD\perp IK\)
\(\Rightarrow\dfrac{1}{AD^2}=\dfrac{1}{AI^2}+\dfrac{1}{AK^2}\)(hệ thức lượng trong tam giác vuông) mà \(AI=AE\left(cmt\right)\Rightarrow\dfrac{1}{AD^2}=\dfrac{1}{AE^2}+\dfrac{1}{AK^2}\) mà hình vuông ABCD không đổi \(\Rightarrow\) AD không đổi\(\Rightarrow\dfrac{1}{AD^2}=\dfrac{1}{AE^2}+\dfrac{1}{AK^2}\) không đổi
Vậy \(\dfrac{1}{AE^2}+\dfrac{1}{AK^2}\) không đổi khi E thay đổi trên cạnh BC
Hai câu cuối í ẹ chưa nghĩ ra, để sau.

Kẻ tia Ay sao cho \(\widehat{yAD}=15^0\). Tia Ay cắt DC tại E.
Kẻ \(AF\perp DC\left(F\in DC\right)\)
\(\Delta EAD=\Delta IAB\left(g-c-g\right)\)
\(\Rightarrow\left\{{}\begin{matrix}AD=AB\\AE=AI\end{matrix}\right.\) (1)
\(\widehat{EAI}=\widehat{DAB}-\widehat{DAE}-\widehat{IAB}=120^0-15^0-15^0=90^0\)
\(\Rightarrow\dfrac{1}{AE^2}+\dfrac{1}{AK^2}=\dfrac{1}{AF^2}\) (h.t.l. trong \(\Delta AEK\) vuông tại A) (2)
\(\widehat{DAC}+\widehat{DAB}=180^0\) (trong cùng phía, AB // CD)
\(\Rightarrow\widehat{DAC}=60^0\)
\(\Rightarrow\Delta ADC\) đều (AD = DC) có AF là đ.c.
\(\Rightarrow AF=\dfrac{\sqrt{3}}{2}AD\)
\(\Rightarrow\dfrac{1}{AF^2}=\dfrac{4}{3AD^2}\) (3)
(1), (2) và (3) \(\Rightarrow\dfrac{4}{3AB^2}=\dfrac{1}{AI^2}+\dfrac{1}{AK^2}\left(\text{đ}pcm\right)\)
Hình tự vẽ >o<

làm bừa thui,ai tích mình mình tích lại
Số số hạng là :
Có số cặp là :
50 : 2 = 25 ( cặp )
Mỗi cặp có giá trị là :
99 - 97 = 2
Tổng dãy trên là :
25 x 2 = 50
Đáp số : 50

Bài 3:
Xét tứ giác BEDC có góc BEC=góc BDC=90 độ
nên BEDC là tứ giác nội tiếp
=>góc AED=góc ACB
=>ΔAED đồng dạng với ΔACB
=>ED/CB=AE/AC=(cos60)=1/2
=>ED=1/2CB=EM=DM
=>ΔMDE đều

A B C D K I M
Qua đỉnh A vẽ \(AK\perp AI\).
Ta có : \(\widehat{KAD}+\widehat{DAM}=\widehat{BAM}+\widehat{MAD}=90^O\)
\(\Rightarrow\widehat{KAD}=\widehat{BAM}\)
Xét \(\Delta KADvà\Delta MAB\) lần lượt vuông tại D và B , có :
\(\left\{{}\begin{matrix}\widehat{KDA}=\widehat{ABM}=90^0\\AD=AB\left(gt\right)\\\widehat{KAD}=\widehat{BAM}\left(cmt\right)\end{matrix}\right.\)\(\Rightarrow\Delta KAD=\Delta MAB\left(cgv-gnk\right)\)
\(\Rightarrow AK=MA\)
Áp dụng hệ thức lượng vào \(\Delta AKI\) vuông tại A có :
\(\dfrac{1}{AK^2}+\dfrac{1}{AI^2}=\dfrac{1}{a^2}\)
\(\Leftrightarrow\dfrac{1}{AM^2}+\dfrac{1}{AI^2}=\dfrac{1}{a^2}\)

Bài 1:
a)
Áp dụng định lý Pitago:
\(BC=\sqrt{AB^2-AC^2}=\sqrt{10^2-8^2}=6\) (cm)
\(S_{ABC}=\frac{AC.CB}{2}=\frac{AB.CK}{2}\Rightarrow CK=\frac{AC.CB}{AB}=\frac{8.6}{10}=4,8\) (cm)
Áp dụng định lý Pitago:
\(BK=\sqrt{CB^2-CK^2}=\sqrt{6^2-4,8^2}=3,6\) (cm)
\(AK=BA-BK=10-3,6=6,4\) (cm)
b)
\(KH\perp BC, KI\perp AC\Rightarrow \widehat{KHC}=\widehat{KIC}=90^0=\widehat{HCI}\)
Tứ giác $KHCI$ có 3 góc vuông nên là hình chữ nhật.
c)
Xét tam giác $CHK$ và $CKB$ có:
Góc $C$ chung
\(\widehat{CHK}=\widehat{CKB}=90^0\)
\(\Rightarrow \triangle CHK\sim \triangle CKB(g.g)\)
\(\Rightarrow \frac{CH}{CK}=\frac{CK}{CB}\Rightarrow CH.CB=CK^2(1)\)
Hoàn toàn tương tự: \(\triangle CKI\sim \triangle CAK(g.g)\)
\(\Rightarrow \frac{CK}{CA}=\frac{CI}{CK}\Rightarrow CA.CI=CK^2(2)\)
Từ \((1);(2)\Rightarrow CH.CB=CA.CI\) (đpcm)
Bài 1:
d)
Vì \(HK\parallel AC\Rightarrow \frac{BH}{BK}=\frac{BC}{BA}\Rightarrow BH=\frac{BK.BC}{AB}\) (định lý Ta-let)
Tương tự: \(\frac{AI}{AK}=\frac{AC}{AB}\Rightarrow AI=\frac{AK.AC}{AB}\)
\(\Rightarrow \frac{AI}{BH}=\frac{AK}{BK}.\frac{AC}{BC}\)
Xét tam giác $BKC$ và $BCA$ có:
\(\left\{\begin{matrix} \text{góc B chung}\\ \widehat{BKC}=\widehat{BCA}=90^0\end{matrix}\right.\Rightarrow \triangle BKC\sim \triangle BCA(g.g)\)
\(\Rightarrow \frac{BK}{BC}=\frac{BC}{BA}\Rightarrow BK=\frac{BC^2}{BA}\) (cái này là công thức hệ thức lượng quen thuộc, mình chỉ chứng minh lại thôi nhé)
Tương tự: \(AK=\frac{AC^2}{AB}\)
\(\Rightarrow \frac{AK}{BK}=\frac{AC^2}{BC^2}(4)\)
Từ \((3);(4)\Rightarrow \frac{AI}{BH}=\frac{AC^2}{BC^2}.\frac{AC}{BC}=\left(\frac{AC}{BC}\right)^3\) (đpcm)
e)
Áp dụng những công thức thu từ phần d:
\(AB.BH.AI=AB.\frac{BK.BC}{BA}.\frac{AK.AC}{AB}=\frac{AK.BK.BC.AC}{AB}\)
Mà \(AK=\frac{AC^2}{AB}; BK=\frac{BC^2}{AB}\Rightarrow AB.BH.AI=\left(\frac{AC.BC}{AB}\right)^3\)
\(=\left(\frac{2S_{ABC}}{AB}\right)^3=CK^3\) (đpcm)
f)
Ta có: \(S_{KHI}=\frac{KH.KI}{2}=\frac{KM.HI}{2}\)
\(\Rightarrow KM=\frac{KH.KI}{HI}\Rightarrow KM^2=\frac{KH^2.KI^2}{HI^2}\)
\(\Rightarrow \frac{1}{KM^2}=\frac{HI^2}{KH^2.KI^2}=\frac{KH^2+KI^2}{KH^2.KI^2}=\frac{1}{KI^2}+\frac{1}{KH^2}\) (Pitago)
Mà theo phần b ta cm được $KHCI$ là hcn nên \(KI=CH; KH=CI\)
\(\Rightarrow \frac{1}{KM^2}=\frac{1}{CH^2}+\frac{1}{CI^2}\) (đpcm)
