Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Định lí 1 : Nếu tam giác vuông có một góc bằng \(30^0\)thì cạnh đối diện với góc ấy bằng nửa cạnh huyền
Vì \(DP\perp AB\)(giả thiết) \(\Rightarrow\Delta PAD\)vuông tại P
\(\Delta PAD\)vuông tại P có \(\widehat{DAP}=60^0\)(giả thiết)
\(\Rightarrow\widehat{PDA}=30^0\)
Do đó \(2PA=DA\)(định lí 1)
\(\Rightarrow4PA^2=DA^2\)
Vì \(\Delta PAD\)vuông tại P (chứng minh trên)
\(\Rightarrow PA^2+PD^2=AD^2\)(định lí Py-ta-go)
\(\Rightarrow PA^2+4^2=4PA^2\)(thay số)
\(\Rightarrow4PA^2-PA^2=16\)
\(\Rightarrow3PA^2=16\)
\(\Rightarrow PA^2=\frac{16}{3}\Rightarrow PA=\sqrt{\frac{16}{3}}=\frac{4}{\sqrt{3}}\left(cm\right)\)(vì \(PA>0\))
Do đó: \(DA=2PA=2.\frac{4}{\sqrt{3}}=\frac{8}{\sqrt{3}}\left(cm\right)\)
Vì \(CH\perp AB\)(giả thiết)
\(\Rightarrow\Delta CHB\)vuông tại H.
\(\Delta CHB\)vuông tại H có \(\widehat{HCB}=60^0\)(giả thiết)
\(\Rightarrow BC=2HC\)(định lí 1)
\(\Rightarrow BC=2.4\)(thay số)
\(\Rightarrow BC=8\left(cm\right)\)
Vì \(\Delta CHB\)vuông tại H (chứng minh trên)
\(\Rightarrow HB^2+HC^2=BC^2\)(định lí Py-ta-go)
\(\Rightarrow HB^2+4^2=8^2\)(thay số)
\(\Rightarrow HB^2+16=64\)
\(\Rightarrow HB^2=56\Rightarrow HB=\sqrt{56}=2\sqrt{14}\left(cm\right)\)(vì \(HB>0\))
Mặt khác, xét tứ giác DCHP có:
\(DP//CH\)(vì cùng vuông góc với AB)
Và \(DP=CH\)(giả thiết)
\(\Rightarrow\)DCHP là hình bình hành
\(\Rightarrow CD=PH=3\left(cm\right)\)(tính chất).
Ta có:
\(AB=AP+PH+HB\)
\(\Rightarrow AB=\frac{4}{\sqrt{3}}+3+2\sqrt{14}\left(cm\right)\)
Do đó:
\(P_{ABCD}=AB+BC+CD+DA=\)\(\frac{4}{\sqrt{3}}+3+2\sqrt{14}+8+3+\frac{8}{\sqrt{3}}\)(thay số)
\(P_{ABCD}=\frac{12}{\sqrt{3}}+14+2\sqrt{14}=4\sqrt{3}+2\sqrt{14}+14\left(cm\right)\)
Vậy \(P_{ABCD}=4\sqrt{3}+2\sqrt{14}+14\left(cm\right)\)

Đặt AI = x (cm) , (x>0) , IC = y (cm) , (y>0)
Ta có : \(2y^2=18,2015\Rightarrow y=\sqrt{\frac{18,2015^2}{2}}\)
Mặt khác : \(x^2+DI^2=AD^2=14,2014^2\) ; \(y^2+DI^2=CD^2=18,2015^2\)
\(\Rightarrow y^2-x^2=18,2015^2-14,2014^2\Rightarrow x=\sqrt{y^2-18,2015^2+14,2014^2}\)
Từ đó dễ dàng giải tiếp bài toán.

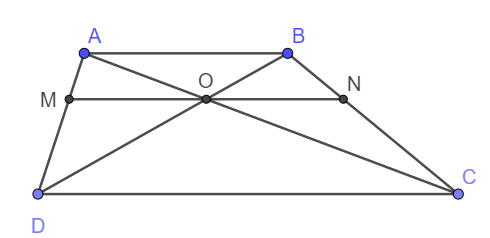
a) Do AB//CD nên áp dụng hệ quả định lý Ta let ta có:
\(\frac{AO}{OC}=\frac{OB}{OD}\) hay \(\frac{DO}{DB}=\frac{OC}{AC}\)
Xét tam giác ABD có OM//AB nên \(\frac{OM}{AB}=\frac{DO}{DB}\)
Tương tự \(\frac{ON}{AB}=\frac{CO}{CA}\)
Vậy nên \(\frac{OM}{AB}=\frac{ON}{AB}\Rightarrow OM=ON\)
b) Coi AB = 1, DC = k thì \(\frac{DO}{OB}=\frac{DC}{AB}=k\Rightarrow\frac{DO}{DB}=\frac{k}{k+1}\)
\(\Rightarrow OM=ON=\frac{k}{k+1}\Rightarrow MN=\frac{2k}{k+1}\)
Ta có \(\frac{1}{AB}+\frac{1}{CD}=\frac{1}{1}+\frac{1}{k}=\frac{k+1}{k}\)
\(\frac{2}{MN}=\frac{2}{\frac{2k}{k+1}}=\frac{k+1}{k}\)
Vậy nên \(\frac{1}{AB}+\frac{1}{CD}=\frac{2}{MN}\)
c) Ta thấy ngay \(\Delta COD\sim\Delta AOB\left(g-g\right)\) theo tỉ lệ k ở câu b.
Vậy thì \(\frac{S_{COD}}{S_{AOB}}=\frac{2009^2}{2008^2}=\left(\frac{2009}{2008}\right)^2=k^2\Rightarrow k=\frac{2009}{2008}\)
Từ đó ta có \(\frac{OC}{OA}=\frac{DO}{OB}=\frac{2009}{2008}\)
Vậy thì \(\frac{S_{ADO}}{S_{AOB}}=\frac{2009}{2008}\Rightarrow S_{ADO}=\frac{2009}{2008}.2008^2=2009.2008\)
\(\frac{S_{BOC}}{S_{AOB}}=\frac{2009}{2008}\Rightarrow S_{BOC}=\frac{2009}{2008}.2008^2=2009.2008\)
Suy ra \(S_{ABCD}=S_{AOB}+S_{DOC}+S_{AOD}+S_{BOC}=2008^2+2009^2+2.2008.2009\)
\(=\left(2008+2009\right)^2=4017^2\left(cm^2\right)\)