Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABD có AM/AB=AQ/AD
nên MQ//BD và MQ=BD/2
Xét ΔCBD có CP/CD=CN/CB
nên NP//BD và NP=BD/2
=>MQ//NP và MQ=NP
=>MNPQ là hình bình hành
b: KHi ABCD là hình thoi thì AC vuông góc với BD
=>MQ vuông góc với MN
=>MNPQ là hình chữ nhật
c: khi ABCD là hình chữ nhật thì AC=BD
=>MN=MQ
=>MNPQ là hình thoi

a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của BC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//AC và MN=AC/2(1)
Xét ΔADC có
Q là trung điểm của AD
P là trung điểm của CD
Do đó: QP là đường trung bình của ΔADC
Suy ra: QP//AC và QP=AC/2(2)
Từ (1) và (2) suy ra MN//PQ và MN=PQ
hay MNPQ là hình bình hành

Lời giải:
$Q,M$ lần lượt là trung điểm của $AD, AB$ nên $QM$ là đường trung bình của tam giác $ADB$ ứng với cạnh $BD$
$\Rightarrow QM\parallel BD$
Tương tự:
$MN\parallel AC, PN\parallel BD, QP\parallel AC$
Do đó:
$MN\parallel PQ\parallel AC$ và $QM\parallel PN\parallel DB$
Tứ giác $MNPQ$ có 2 cặp cạnh đối song song với nhau nên là hình bình hành.
Mà $AC\perp BD$ (do $ABCD$ là hình thoi)
$\Rightarrow QM\perp MN\Rightarrow \widehat{M}=90^0$
Hình bình hành $MNPQ$ có $\widehat{M}=90^0$ nên $MNPQ$ là hình chữ nhật.

a: Xét ΔBAD có
M,Q lần lượt là tđiểm của AB và AD
nên MQ là đường trung bình
=>MQ//BD và MQ=BD/2(1)
Xét ΔBCD có
N,P lần lượt là trung điểm của CB và CD
nên NP là đường trung bình
=>NP//BD và NP=BD/2(2)
Từ (1) và (2) suy a MQ//NP và MQ=NP
=>MNPQ là hình bình hành
b: Xét ΔABC có
M,N lần lượt là trung điểm của BA và BC
nên MN là đường trung bình
=>MN=AC/2 và MN//AC
Để MNPQ là hình chữ nhật thì MN vuông góc với MQ
=>AC vuông góc với BD

a: Xét ΔABD có
M là trung điểm của AB
Q là trung điểm của AD
Do đó: MQ là đường trung bình của ΔABD
Suy ra: MQ//BD và MQ=BD/2(1)
Xét ΔBCD có
N là trung điểm của BC
P là trung điểm của CD
Do đó: NP là đường trung bình của ΔBCD
Suy ra: NP//BD và NP=BD/2(2)
Từ (1) và (2) suy ra MQ//NP và MQ=NP
hay MQPN là hình bình hành

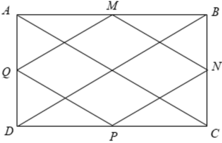
M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, AD
⇒ AM = MB; BN = NC; CP = DP; AQ = DQ
+ Xét Δ ABD có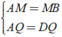
⇒ MQ là đường trung bình của Δ ABD.
⇒ QM = 1/2BD = 1/2AC ( 1 )
+ Xét Δ ABC có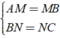
⇒ MN là đường trung bình của Δ ABC.
⇒ MN = 1/2BD = 1/2AC ( 2 )
+ Xét Δ BCD có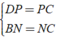
⇒ NP là đường trung bình của Δ BCD.
⇒ NP = 1/2BD = 1/2AC ( 3 )
+ Xét Δ ADC có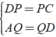
⇒ QP là đường trung bình của Δ ADC.
⇒ QP = 1/2BD = 1/2AC ( 4 )
Từ ( 1 ),( 2 ),( 3 ),( 4 ) ⇒ MN = NP = PQ = QM.
⇒ MNPQ là hình thoi.

A B D C M N P Q Xét △ADC có:
AQ=QD và DP=PC
=>QP là đường trung bình=>QP//AC và QP=1/2 AC
Xét △ABC có:
AM=MB và BN=NC
=>MN là đường trung bình=>MN//AC và MN=1/2 AC
=>MN//QP và MN=QP
=>MNPQ là hbh
Xét △ABD có :
AQ=QD và MA=MB
=>QM là đường trung bình
=>QM=1/2 BD
Mà AC=BD (do ABCD là hcn)
=>QM=1/2 AC
=>QM=QP
=>MNPQ là h.thoi

Xét ΔADB có
M là trung điểm của AB
Q là trung điểm của AD
Do đó: MQ là đường trung bình
=>MQ//BD và MQ=BD/2(1)
Xét ΔBCD có
N là trung điểm của BC
P là trung điểm của CD
Do đó: NP là đường trung bình
=>NP//BD và NP=BD/2(2)
Từ (1) và (2) suy ra MQ//NP và MQ=NP(3)
Xét ΔABC có
M là trung điểm của AB
N là trung điểm của BC
Do đó: MN là đường trung bình
=>MN=AC/2
mà MQ=BD/2
mà AC=BD
nên MN=MQ(4)
Từ (3) và (4) suy ra MNPQ là hình thoi
Xét Δ AQN và Δ MBN có :
\(\widehat{QAM}=\widehat{MBN}=90^o\)
\(AM=BM\) (M là trung điểm AB)
\(AQ=BN\) (Q;N là trung điểm AD;BC và AD=BC)
⇒ Δ AQN và Δ MBN (cạnh, góc, cạnh)
\(\Rightarrow QM=MN\left(1\right)\)
Chứng minh tương tự :
- Δ AQN và Δ QDP (cạnh, góc, cạnh) \(\Rightarrow QM=QP\left(2\right)\)
- Δ PNC và Δ QDP (cạnh, góc, cạnh) \(\Rightarrow PN=QP\left(3\right)\)
- Δ PNC và Δ MBN (cạnh, góc, cạnh) \(\Rightarrow PN=MN\left(4\right)\)
\(\left(1\right);\left(2\right);\left(3\right);\left(4\right)\Rightarrow QM=MN=PN=QP\)
⇒ Tứ giác MNQP là hình thoi (dpcm)