K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

HT
28 tháng 12 2020
a/ \(\left\{{}\begin{matrix}S=\left(SAB\right)\cap\left(SCD\right)\\Sx//AB//CD\end{matrix}\right.\Rightarrow\left(SAB\right)\cap\left(SCD\right)=Sx\)
b/ \(\left(MCD\right)\cap\left(ABCD\right)=CD\)
\(\left(MCD\right)\cap\left(SBC\right)=MC\)
\(\left(MCD\right)\cap\left(SCD\right)=CD\)
\(\left(MCD\right)\cap\left(SAB\right)=My\left(My//AB//CD\right)\)
\(\Rightarrow TD:CDM\)
Vậy thiết diện là hình tam giác.
P/s: Chắc bạn sẽ thắc mắc tại sao lại ko xét trường hợp (MCD) cắt (SAD). Bởi vì chúng ko có giao tuyến :)
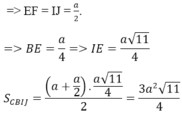
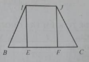
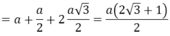

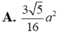
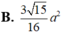
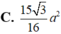

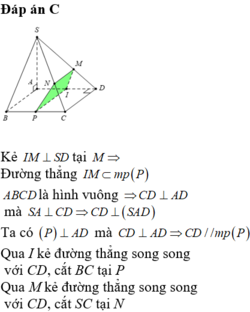



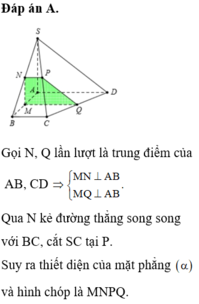

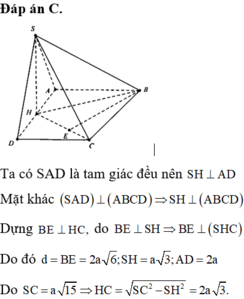
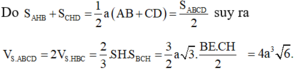
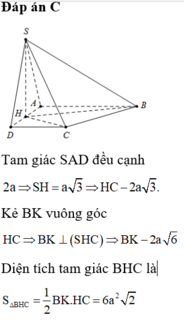
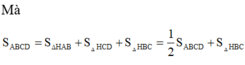
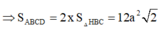
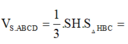
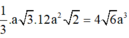
trong mặt phẳng (SAC) : SO ∩ CI = K là trọng tâm tam giác SAC
Trong mặt phẳng (SBD): BK ∩ SD = J là trung điểm SD ⇒ IJ // AD ⇒ IJ // BC.
∆SAB = ∆SCD (c.c.c) ⇒ trung tuyến BI = CJ ⇒ thiết diện CBIJ là hình thang cân.
Đáp án D