Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Do AB song song Cd
=> Áp dụng định lí Ta - lét được \(\frac{AB}{DG}=\frac{AE}{EG}=\frac{BE}{DE}\)
=> AB . EG = DG . AE
Do AD song song BK nên áp dụng định lí Ta lét được
\(\frac{AE}{AK}=\frac{DE}{BD}\)
Do AB sog song với CG nên áp dụng định lí Ta lét được
\(\frac{AE}{AG}=\frac{BE}{BD}\)
=> \(\frac{AE}{AK}+\frac{AE}{AG}=\frac{BE}{BD}+\frac{DE}{BD}=1\)
=>\(\frac{1}{AE}=\frac{1}{AK}+\frac{1}{AG}\)
Ta có \(\frac{BK}{AD}=\frac{AB}{DG}=\frac{BE}{DE}\)
=>\(BK.DG=AB.AD\left(KHÔNG\right)DOI\)

A B D C E G K a b
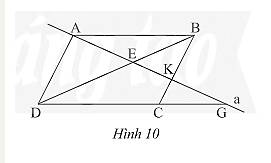
a) Vì ABCD là hình bình hành ( gt )
Và K thuộc BC nên
AD // BK Theo hệ quả của định lý Ta-let ta có :
\(\frac{EK}{AE}=\frac{EB}{ED}=\frac{AE}{EG}\Rightarrow\frac{EK}{AE}=\frac{AF}{EG}\Rightarrow AE^2=EK.EG\)
b) Ta có :
\(\frac{AE}{EK}-\frac{DE}{DB};\frac{AE}{AG}=\frac{BE}{BD}\)nên
\(\frac{AE}{AK}+\frac{AE}{AG}-\frac{BE}{BD}+\frac{DE}{DB}-\frac{BD}{BD}-1\Rightarrow\frac{1}{AE}=\frac{1}{AK}+\frac{1}{AG}\)
c) bạn tự làm tiếp mỏi tay quá

Giải nốt bài của Pác Hiếu:3
Đặt \(AB=a',AD=b\)
Áp dụng Đ/L Thales vào tam giác ABK,ta có:
\(\frac{BK}{KC}=\frac{AB}{CG}\Rightarrow\frac{a'}{CG}=\frac{BK}{KC}\left(1\right)\)
Áp dụng Đ/L Thales vào tam giác ADG,ta có:
\(\frac{CG}{DG}=\frac{CK}{AD}\Rightarrow\frac{CG}{DG}=\frac{CK}{b}\left(2\right)\)
Nhân vế theo vế của (1);(2) ta có:
\(\frac{BK}{b}=\frac{a'}{DG}\Rightarrow BK\cdot DG=a'b\) không đổi.

a) Vì \(ABCD\) là hình bình hành nên \(AB//CD;AD//BC\)
\( \Rightarrow AB//DG;AB//CG;BK//AD;KC//AD\)
Xét tam giác \(DEG\) có \(AB//DG\), theo hệ quả của định lí Thales ta có:
\(\frac{{AE}}{{EG}} = \frac{{EB}}{{ED}}\) (1)
Xét tam giác \(ADE\) có \(BK//AD\), theo hệ quả của định lí Thales ta có:
\(\frac{{EK}}{{AE}} = \frac{{EB}}{{ED}}\) (2)
Từ (1) và (2) suy ra, \(\frac{{AE}}{{EG}} = \frac{{EK}}{{AE}} \Rightarrow A{E^2} = EG.EK\) (điều phải chứng minh).
b) Xét tam giác \(AED\) có:
\(AD//BK \Rightarrow \frac{{AE}}{{AK}} = \frac{{DE}}{{DB}}\)(3)
Xét tam giác \(AEB\) có
\(AB//BK \Rightarrow \frac{{AE}}{{AG}} = \frac{{BE}}{{BD}}\) (4)
Từ (3) và (4) ta được:
\(\frac{{AE}}{{AK}} + \frac{{AE}}{{AG}} = \frac{{DE}}{{BD}} + \frac{{BE}}{{BD}} = \frac{{BD}}{{BD}} = 1\)
Ta có: \(\frac{{AE}}{{AK}} + \frac{{AE}}{{AG}} = 1 \Rightarrow \frac{1}{{AE}} = \frac{1}{{AK}} + \frac{1}{{AG}}\) (chia cả hai vế cho \(AE\)) (điều phải chứng minh).

a) vì tứ giác ABCD là hình bình hành
=> AB // CD
=>AB // DG
=>EB/ED = AE/EG (1)
vì ABCD là hình bình hành
=> AD // BC
=> AD // BK
=>AE/EG = EK/AE (2)
TỪ (1) VÀ (2)
=> AE/EG = EK/AE
=> AE ^2 = EK . EG (đpcm)
b) vì AB // DG
=> AE/AG = BE/BD
MÀ AD // BK
=> AE /AK= DE /BD
CỘNG 2 VẾ TRÊN
=> AE/AG + AE/AK = BE/BD + DE/BD = 1
<=> AE ( 1/AG + 1/AK ) = 1
<=> 1/AG + 1/AK = AE 1 (đpcm)
c) vì AD // BK
=> BK/AD = EB/DE
CÓ AB // DG
=> AB/DG = BE /DE
=> BK/AD = AB/DG
=> BD . DG = AB . AD mà AB, AD là các cạnh của hình bình hành ABCD
=> AB . AD không đổi
=> BK . DG không đổi (đpcm)
A B C D E K G
Áp dụng hệ quả định lí Thales,ta có :
\(\Delta EBK\)có AD // BK\(\Rightarrow\frac{AE}{AK}=\frac{DE}{BD}\left(1\right);\frac{BK}{AD}=\frac{BE}{DE}\left(2\right)\)
\(\Delta DEG\)có AB // DG\(\Rightarrow\frac{AE}{AG}=\frac{BE}{BD}\left(3\right);\frac{AB}{DG}=\frac{BE}{DE}\left(4\right)\)
Từ (1) và (3),ta có :\(\frac{AE}{AK}+\frac{AE}{AG}=\frac{DE}{BD}+\frac{BE}{BD}=\frac{BD}{BD}=1\Rightarrow\frac{1}{AK}+\frac{1}{AG}=\frac{1}{AE}\)
Từ (2) và (4),ta có \(\frac{BK}{AD}=\frac{AB}{DG}\)=> BK.DG = AB.AD = 3.5 = 15 (cm)
mình cũng vậy