Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(f'\left(x\right)=1-\dfrac{2x}{\sqrt{x^2+12}}\le0\\ \Leftrightarrow\sqrt{x^2+12}\le2x\\ \Leftrightarrow\left\{{}\begin{matrix}x^2+12\le4x^2\\x\ge0\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}3x^2\ge12\\x\ge0\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x^2\ge4\\x\ge0\end{matrix}\right.\Leftrightarrow x\ge2\)
Đáp số : \(\left[2,+\infty\right]\)

Lời giải:
a) Ta có f'(x) = 3x2 + 1, g(x) = 6x + 1. Do đó
f'(x) > g'(x) <=> 3x2 + 1 > 6x + 1 <=> 3x2 - 6x >0
<=> 3x(x - 2) > 0 <=> x > 2 hoặc x > 0 <=> x ∈ (-∞;0) ∪ (2;+∞).
b) Ta có f'(x) = 6x2 - 2x, g'(x) = 3x2 + x. Do đó
f'(x) > g'(x) <=> 6x2 - 2x > 3x2 + x <=> 3x2 - 3x > 0
<=> 3x(x - 1) > 0 <=> x > 1 hoặc x < 0 <=> x ∈ (-∞;0) ∪ (1;+∞).

\(C'=0\) với mọi hằng số C
nguyen thi khanh nguyen
\(f'\left(x\right)=6x^2-2x\)
\(g'\left(x\right)=3x^2+x\)
\(f'\left(x\right)>g'\left(x\right)\Leftrightarrow6x^2-2x>3x^2+x\)
\(\Leftrightarrow3x^2-3x>0\Rightarrow\left[{}\begin{matrix}x>1\\x< 0\end{matrix}\right.\)

a) \(x=-45^0+k90^0,k\in\mathbb{Z}\)
b) \(x=-\dfrac{\pi}{6}+k\pi,k\in\mathbb{Z}\)
c) \(x=\dfrac{3\pi}{4}+k2\pi,k\in\mathbb{Z}\)
d) \(x=300^0+k540^0,k\in\mathbb{Z}\)

a) Cách 1: y' = (9 -2x)'(2x3- 9x2 +1) +(9 -2x)(2x3- 9x2 +1)' = -2(2x3- 9x2 +1) +(9 -2x)(6x2 -18x) = -16x3 +108x2 -162x -2.
Cách 2: y = -4x4 +36x3 -81x2 -2x +9, do đó
y' = -16x3 +108x2 -162x -2.
b) y' = .(7x -3) +
(7x -3)'=
(7x -3) +7
.
c) y' = (x -2)'√(x2 +1) + (x -2)(√x2 +1)' = √(x2 +1) + (x -2) = √(x2 +1) + (x -2)
= √(x2 +1) +
=
.
d) y' = 2tanx.(tanx)' - (x2)' =
.
e) y' = sin
=
sin
.
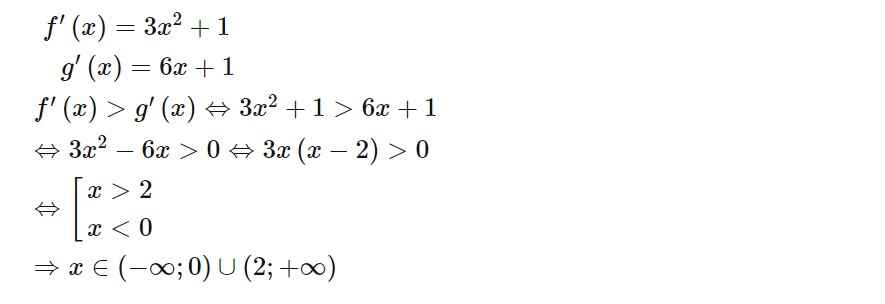
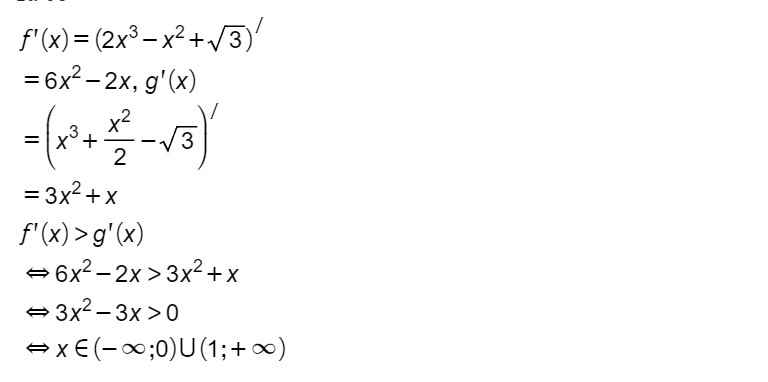
Bài giải
ĐKXĐ của hàm số \(\int'\left(x\right)\)là x < -2 hoac x > 4 .
Vậy ta phải giải bất phương trình
\(\int'\left(x\right)=\dfrac{x-1}{\sqrt{x^2-2x-8}}\le1\)(vs x < -2 hoac x > 4 ) .
\(\odot\) Vs x < -2 thì x - 1 < 0 , do đó :
\(\int'\left(x\right)\le1\Leftrightarrow\sqrt{x^2-2x-8}\)
\(\Leftrightarrow\left(x-1\right)^2\le x^2-2x-8\Leftrightarrow1\le-8\) ( loại )
Vậy đáp số của bài toán là x < -2.
@CÔNG CHÚA THẤT LẠC