Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chào bạn, mình từng làm bài này giúp một bạn khác rồi, link đây nhé:
https://hoc24.vn/hoi-dap/question/778686.html

Ta có:
\(Q=\dfrac{2002}{a}+\dfrac{2017}{b}+2996a-5501b\)
\(=\left(\dfrac{2002}{a}+8008a\right)+\left(\dfrac{2017}{b}+2017b\right)-\left(5012a+7518b\right)\)
\(=\left(\dfrac{2002}{a}+8008a\right)+\left(\dfrac{2017}{b}+2017b\right)-2506\left(2a+3b\right)\)
Áp dụng BĐT Cauchy cho hai số không âm ta có:
\(\dfrac{2002}{a}+8008a\ge2\sqrt{\dfrac{2002}{a}.8008a}=2.4004=8008\) (1)
\(\dfrac{2017}{b}+2017b\ge2\sqrt{\dfrac{2017}{b}.2017b}=2.2017=4034\) (2)
Có \(2a+3b\le4\Rightarrow-\left(2a+3b\right)\ge-4\Rightarrow-2506\left(2a+3b\right)\ge-10024\)(3)
Từ (1), (2) và (3) \(\Rightarrow Q\ge8008+4034-10024=2018\)
Dấu '=' xảy ra \(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2002}{a}=8008a\\\dfrac{2017}{b}=2017b\\2a+3b=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{1}{2}\\b=1\end{matrix}\right.\)
Vậy,...
![]()

\(Q=\frac{2002}{a}+8008a+\frac{2017}{b}+2017b-2506\left(2a+3b\right)\)
\(Q\ge2\sqrt{\frac{2002}{a}.8008a}+2\sqrt{\frac{2017}{b}.2017b}-2506.4\)
\(Q\ge2018\)
\(\Rightarrow Q_{min}=2018\) khi \(\left\{{}\begin{matrix}a=\frac{1}{2}\\b=1\end{matrix}\right.\)

Ta có
Q = 2002 1 a + 4 a + 2017 1 b + b − 5012 a − 7518 b = 2002 1 a + 4 a + 2017 1 b + b − 2506 2 a + 3 b
+ Vì a, b dương và 2 a + 3 b ≤ 4 ⇒ 0 < 2 a + 3 b ≤ 4 do đó
Q ≥ 2002.2. 1 a .4 a + 2017.2. 1 b . b − 2506.4 = 2018 với mọi a, b>0 và 2 a + 3 b ≤ 4 , dấu bằng xảy ra khi a = 1 2 và b= 1.
+ Vậy giá trị nhỏ nhất của Q bằng 2018 khi a = 1 2 và b= 1..

\(P=2a+\dfrac{9}{a}+3b+\dfrac{2}{b}=\left(a+\dfrac{9}{a}\right)+\left(2b+\dfrac{2}{b}\right)+\left(a+b\right)\)
\(\ge2\sqrt{a.\dfrac{9}{a}}+2\sqrt{2b.\dfrac{2}{b}}+=6+4+4=14\)
Dấu "=" xảy ra \(\Leftrightarrow\left\{{}\begin{matrix}a=3\\b=1\end{matrix}\right.\)

Ta có: P= \(2a+3b+\dfrac{1}{a}+\dfrac{4}{b}\) = \(\text{}\text{}(\dfrac{1}{a}+a)+\left(\dfrac{4}{b}+b\right)+\left(a+2b\right)\)
Ta thấy: \(\text{}\text{}(\dfrac{1}{a}+a)\ge2\sqrt{\dfrac{1}{a}\cdot a}=2\)
\(\text{}\text{}\left(\dfrac{4}{b}+b\right)\ge2\sqrt{\dfrac{4}{b}\cdot b}=4\)
Do đó: P \(\ge2+4+8=14\)
Vậy: P(min)=14 khi: \(\left\{{}\begin{matrix}\dfrac{1}{a}=a\\\dfrac{4}{b}=b\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=1\\b=2\end{matrix}\right..\)

Bài làm
\(P=2a+3b+\frac{4}{a}+\frac{9}{b}=a+a+2b+b+\frac{4}{a}+\frac{9}{b}\)
\(=\left(a+2b\right)+\left(a+\frac{4}{a}\right)+\left(b+\frac{9}{b}\right)\)
\(\ge8+2\sqrt{a\times\frac{4}{a}}+2\sqrt{b\times\frac{9}{b}}\)( Cauchy )
\(=8+4+6=18\)
Đẳng thức xảy ra khi a = 2 ; b = 3
=> MinP = 18 <=> a = 2 ; b = 3
\(P=2a+3b+\frac{4}{a}+\frac{9}{b}\)
\(\Leftrightarrow P=\left(a+\frac{4}{a}\right)+\left(b+\frac{9}{b}\right)+a+2b\)
Áp dụng BĐT AM-GM ta có:
\(P\ge2.\sqrt{a.\frac{4}{a}}+2.\sqrt{b.\frac{9}{b}}+a+2b=2.2+2.3+a+2b\ge4+6+8=18\)
Dấu " = " xảy ra \(\Leftrightarrow\hept{\begin{cases}a=\frac{4}{a}\\b=\frac{9}{b}\end{cases}}\Leftrightarrow\hept{\begin{cases}a=2\\b=3\end{cases}}\)
Vậy \(P_{min}=18\)\(\Leftrightarrow\hept{\begin{cases}a=2\\b=3\end{cases}}\)
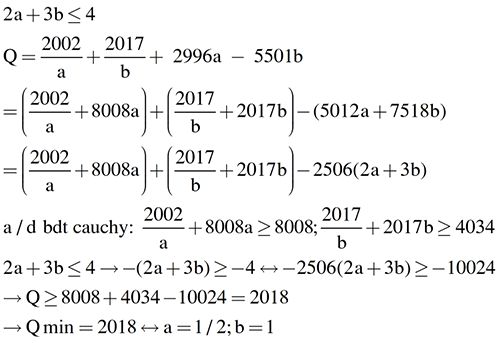
\(Q=\dfrac{2002}{a}+\dfrac{2017}{b}+2996a-5501b=\left(\dfrac{2002}{a}+8008a\right)+\left(\dfrac{2017}{b}+2017b\right)-\left(5012a+7518b\right)\)
\(=\left(\dfrac{2002}{a}+8008a\right)+\left(\dfrac{2017}{b}+2017b\right)-2506\left(2a+3b\right)\)
Áp dụng bất đẳng thức Cosi cho 2 số dương:
\(\left\{{}\begin{matrix}\dfrac{2002}{a}+8008\ge2\sqrt{\dfrac{2002}{a}.8008}=8008\\\dfrac{2017}{b}+2017b\ge2\sqrt{\dfrac{2017}{b}.2017b}=4034\end{matrix}\right.\)
Ta có: \(2a+3b=4\Rightarrow-\left(2a+3b\right)=-4\Leftrightarrow-2506\left(2a+3b\right)=-10024\)
\(\Rightarrow Q\ge8008+4034-10024=2018\)
\(ĐTXR\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{1}{2}\\b=1\end{matrix}\right.\)