Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng định lí cosin trong tam giác ABC, ta có:
\(\begin{array}{l}{c^2} = {b^2} + {a^2} - 2ab\cos C\\ \Leftrightarrow {c^2} = 26,{4^2} + 49,{4^2} - 2.26,4.49,4\cos {47^ \circ }20'\\ \Rightarrow c \approx 37\end{array}\)
Áp dụng định lí sin, ta có: \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}}\)
\(\begin{array}{l} \Leftrightarrow \frac{{49,4}}{{\sin A}} = \frac{{26,4}}{{\sin B}} = \frac{{37}}{{\sin {{47}^ \circ }20'}}\\ \Rightarrow \sin A = \frac{{49,4.\sin {{47}^ \circ }20'}}{{37}} \approx 0,982 \Rightarrow \widehat A \approx {79^ \circ }\\ \Rightarrow \widehat B \approx {180^ \circ } - {79^ \circ } - {47^ \circ }20' = {53^ \circ }40'\end{array}\)

a) Phương trình tham số của đường thẳng \(d:\left\{ \begin{array}{l}x = 1 + 40t\\y = 1 + 30t\end{array} \right.\)
b) Thay \(t = 2\) vào phương trình\(d:\left\{ \begin{array}{l}x = 1 + 40t\\y = 1 + 30t\end{array} \right.\) ta được \(\left\{ \begin{array}{l}x = 1 + 40.2 = 81\\y = 1 + 30.2 = 61\end{array} \right.\)
Vậy khi \(t = 2\) thì tọa độ của ô tô là \(\left( {81;61} \right)\)
Thay \(t = 4\) vào phương trình\(d:\left\{ \begin{array}{l}x = 1 + 40t\\y = 1 + 30t\end{array} \right.\) ta được \(\left\{ \begin{array}{l}x = 1 + 40.4 = 161\\y = 1 + 30.4 = 121\end{array} \right.\)
Vậy khi \(t = 4\) thì tọa độ của ô tô là \(\left( {161;121} \right)\)

a) Áp dụng định lí cosin, ta có:
\(\begin{array}{l}{a^2} = {b^2} + {c^2} - 2bc.\cos A\\ \Leftrightarrow {a^2} = {8^2} + {5^2} - 2.8.5.\cos {120^ \circ } = 129\\ \Rightarrow a = \sqrt {129} \end{array}\)
Áp dụng định lí sin, ta có:
\(\begin{array}{l}\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} \Rightarrow \frac{{\sqrt {129} }}{{\sin {{120}^ \circ }}} = \frac{8}{{\sin B}} = \frac{5}{{\sin C}}\\ \Rightarrow \left\{ \begin{array}{l}\sin B = \frac{{8.\sin {{120}^ \circ }}}{{\sqrt {129} }} \approx 0,61\\\sin C = \frac{{5.\sin {{120}^ \circ }}}{{\sqrt {129} }} \approx 0,38\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\widehat B \approx 37,{59^ \circ }\\\widehat C \approx 22,{41^ \circ }\end{array} \right.\end{array}\)
b) Diện tích tam giác ABC là: \(S = \frac{1}{2}bc.\sin A = \frac{1}{2}.8.5.\sin {120^ \circ } = 10\sqrt 3 \)
c)
+) Theo định lí sin, ta có: \(R = \frac{a}{{2\sin A}} = \frac{{\sqrt {129} }}{{2\sin {{120}^ \circ }}} = \sqrt {43} \)
+) Đường cao AH của tam giác bằng: \(AH = \frac{{2S}}{a} = \frac{{2.10\sqrt 3 }}{{\sqrt {129} }} = \frac{{20\sqrt {43} }}{{43}}\)

Gọi độ dài cạnh OB là x cm \(\left( {x > 0} \right)\)
Theo giả thiết ta có \(AB = BC = OB - 1 = x - 1\)
Áp dụng định lý pitago trong tam giác vuông OAB và OBC ta có:
\(OC = \sqrt {O{B^2} + B{C^2}} = \sqrt {{x^2} + {{\left( {x - 1} \right)}^2}} = \sqrt {2{x^2} - 2x + 1} \)
\(OA = \sqrt {O{B^2} - A{B^2}} = \sqrt {{x^2} - {{\left( {x - 1} \right)}^2}} = \sqrt {2x - 1} \)
a) \(OC = 3OA \Rightarrow \sqrt {2{x^2} - 2x + 1} = 3\sqrt {2x - 1} \)
\(\begin{array}{l} \Rightarrow 2{x^2} - 2x + 1 = 9\left( {2x - 1} \right)\\ \Rightarrow 2{x^2} - 20x + 10 = 0\end{array}\)
\( \Rightarrow \)\(x = 5 - 2\sqrt 5 \) và \(x = 5 + 2\sqrt 5 \)
Thay hai nghiệm vừa tìm được vào phương trình \(\sqrt {2{x^2} - 2x + 1} = 3\sqrt {2x - 1} \) ta thấy cả hai đều thỏa mãn phương trình
Vậy khi \(OB = 5 - 2\sqrt 5 \) hoặc \(OB = 5 + 2\sqrt 5 \)thì \(OC = 3OA\)
b) \(OC = \frac{5}{4}OB \Rightarrow \sqrt {2{x^2} - 2x + 1} = \frac{5}{4}x\)
\(\begin{array}{l} \Rightarrow 2{x^2} - 2x + 1 = \frac{{25}}{{16}}{x^2}\\ \Rightarrow \frac{7}{{16}}{x^2} - 2x + 1 = 0\end{array}\)\(\)
\( \Rightarrow x = \frac{4}{7}\) hoặc \(x = 4\)
Thay hai nghiệm vừa tìm được vào phương trình \(\sqrt {2{x^2} - 2x + 1} = \frac{5}{4}x\) ta thấy cả hai nghiệm đều thỏa mãn phương trình
Vậy khi \(OB = \frac{4}{7}\) hoặc \(OB = 4\) (cm) thì \(OC = \frac{5}{4}OB\)

Vì ABCD là hình bình hành nên ta có: \(\overrightarrow {AD} = \overrightarrow {BC} \)\(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \) (đpcm)

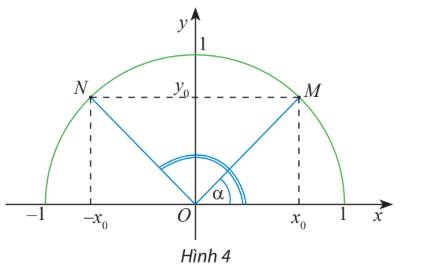
Gọi H là hình chiếu vuông góc của N Ox.
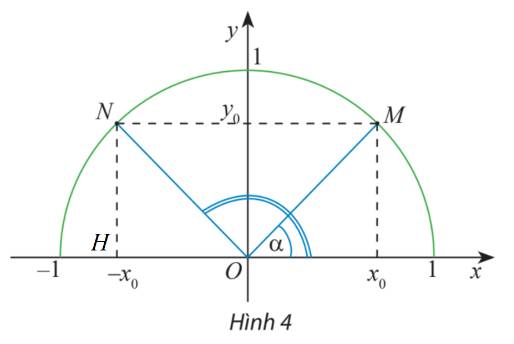
Ta có: \(\widehat {NOH} = \widehat {ONM} = \widehat {OMN} = \widehat {MOx} = \alpha \) (do NM song song với Ox)
Mà \(\widehat {xOM} + \widehat {NOH} = {180^o}\)
Suy ra \(\widehat {xON} + \widehat {MOx} = {180^o}\)

Xét tam giác APB và AQB, ta có:
\(\tan {35^ \circ } = \frac{{AB}}{{PB}} = \frac{{AB}}{{300 + QB}}\) và \(\tan {48^ \circ } = \frac{{AB}}{{QB}}\)
\(\begin{array}{l} \Rightarrow AB = \tan {35^ \circ }.\left( {300 + QB} \right) = \tan {48^ \circ }.QB\\ \Leftrightarrow \tan {35^ \circ }.300 + \tan {35^ \circ }.QB = \tan {48^ \circ }.QB\\ \Leftrightarrow \tan {35^ \circ }.300 = \left( {\tan {{48}^ \circ } - \tan {{35}^ \circ }} \right).QB\\ \Leftrightarrow QB = \frac{{\tan {{35}^ \circ }.300}}{{\tan {{48}^ \circ } - \tan {{35}^ \circ }}}\end{array}\)
Mà \(AB = \tan {48^ \circ }.QB\)
\( \Rightarrow AB = \tan {48^ \circ }.\frac{{\tan {{35}^ \circ }.300}}{{\tan {{48}^ \circ } - \tan {{35}^ \circ }}} \approx 568,5\;(m)\)
Vậy tháp hải đăng cao khoảng 568,5 m.

a) \(23,3\) phút; \(540^0;27,6^0C\)
b) Khi lấy số trung bình làm đại diện cho các số liệu thống kê về quy mô và độ lớn, có thể xem rằng mỗi ngày bạn A đi từ nhà đến trường đều mất 23,3 phút.
Tương tự, nêu ý nghĩa số trung bình của các số liệu thống kê cho ở bảng 7 và bảng 8.

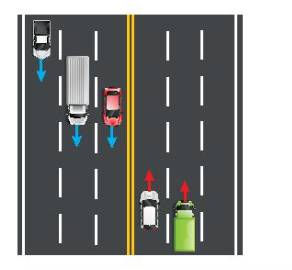
a) Các làn đường song song với nhau: Đúng.
b) Các xe chạy theo cùng một hướng: Sai.
Trong hình 4.5: Có 3 xe chạy theo hướng từ trên xuống dưới, 2 xe chạy thep hướng từ dưới lên trên
c) Hai xe bất kì đều chạy theo cùng một hướng hoặc hai hướng ngược nhau: Đúng.
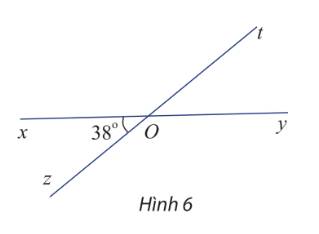






Ta có hai góc \(\widehat {xOz}\) và \(\widehat {tOy}\) đối đỉnh nên \(\widehat {xOz} = \widehat {tOy} = 38^\circ \)
hai góc \(\widehat {xOt}\) và \(\widehat {yOz}\) đối đỉnh nên \(\widehat {xOt} = \widehat {yOz}\)
\(\widehat {xOz}\) và \(\widehat {xOt}\) bù nhau nên \(\widehat {xOt} = 180^\circ - \widehat {xOz} = 180^\circ - 38^\circ = 142^\circ \)
Vậy \(\widehat {xOz} = \widehat {tOy} = 38^\circ \) và \(\widehat {xOt} = \widehat {yOz} = 142^\circ \)