Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

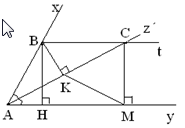
A x y z t B H C M K Ta có Bt song song vs Ay => góc KAH = góc ACB= 30 độ( so le trong) mà KAH= KAB=30 độ (gt) => KAB= BCA = 30 độ => tâm gics ABC cân ở B
Xét tam giác ABK và tam giác CBK:
góc KAB= góc CKB=90 độ
AB=BC( tam giác ABC cân)
góc KAB= góc BCA => tam giác ABK= tam giác CBK( ch-gn)
=> KA=KC => K là trung điểm của AC
b) góc A= 60 độ => góc ABK= 60 độ ( góc KAB+ góc AKB = 30 độ+ 90 độ=120 độ)(1), AB chung(2) , HAB=AKB=90 độ (3)
Từ (1),(2),(3)=> tam giác ABH= tam giác ABK( ch-gn)=> BH=AK mà AK=KC=1/2AC =>BH=1/2 AC
c) góc KBA= 120 độ => KBC= 60 độ( kề bù)
xét tam giác ABH và tam giác CBK có :
góc AHB= góc BKC= 90 độ
góc A= góc KBC= 60 độ
AB=CB => tam giác =tam giác (ch-gn)
MH vuông góc vs BH, MH vuông góc vs CM =>HB song song vs CM
=> BH=CM (t/c đoạn chắn)
=>CK=CM mà KCM=60 độ( M=90 độ góc MAC=30 độ)
=> tam giác KMC đều

x A y z B C H K M
a. Ta có: BC//Ay(gt)\(\Rightarrow\widehat{BCA}=\widehat{MAC}\) (2 góc so le trong)
Mà: \(\widehat{MAC}=\widehat{CAB}=\frac{60^o}{2}=30^o\) ( vì AC là tia phân giác \(\widehat{xAy}\) )
\(\Rightarrow\widehat{BAC}=\widehat{BCA}\Rightarrow\Delta BAC\) cân tại B
Xét \(\Delta BAC\) cân tại B, có: BK là đường cao
\(\Rightarrow\) BK là đường trung tuyến
\(\Rightarrow K\) là trung điểm AC
b. Xét \(\Delta HAB\) có: \(\widehat{HBA}=180^o-90^o-60^o=30^o\)
Mà: \(\widehat{KAB}=30^o\left(cmt\right)\)
\(\Rightarrow\widehat{HBA}=\widehat{KAB}\left(=30^o\right)\)
Xét \(\Delta KAB\left(\widehat{K}=90^o\right)\) và \(\Delta HBA\left(\widehat{H}=90^o\right)\) có:
\(AB\) chung
\(\widehat{HBA}=\widehat{KAB}\left(cmt\right)\)
\(\Rightarrow\Delta KAB=\Delta HBA\left(ch-gn\right)\)
\(\Rightarrow BH=AK\) ( 2 cạnh tương ứng )
Mà: \(AK=\frac{AC}{2}\)
\(\Rightarrow BH=\frac{AK}{2}\)
a) Vì \(Az\) là tia phân giác của \(\widehat{BAM}\left(gt\right)\)
=> \(K\) là trung điểm của \(AC.\)
b) Vì \(K\) là trung điểm của \(AC\left(cmt\right).\)
=> \(AK=\frac{1}{2}AC\) (tính chất trung điểm).
Vì \(Az\) là tia phân giác của \(\widehat{BAH}\left(gt\right)\)
Mà \(AK=\frac{1}{2}AC\left(cmt\right)\)
=> \(BH=\frac{1}{2}AC.\)
Hay \(BH=\frac{AC}{2}.\)
c) Ta có:

a)Xét △BKA có:
\(\widehat{BKA}+\widehat{BAK}+\widehat{KBA}=180^0\)
\(\Rightarrow90^0+30^0+\widehat{KBA}=180^0\Rightarrow\widehat{KBA}=180^0-90^0-30^0=60^0\) (1)
Xét △BKC có:
\(\widehat{BKC}+\widehat{BCK}+\widehat{KBC}=180^0\)
\(\Rightarrow90^0+30^0+\widehat{KBC}=180^0\Rightarrow\widehat{KBC}=180^0-90^0-30^0=60^0\) (2)
Từ (1) và (2)\(\Rightarrow\widehat{KBA}=\widehat{KBC}\) Xét △BKA và △BKC có: \(\widehat{BKA}=\widehat{BKC}\left(=90^0\right)\)BK chung
\(\widehat{KBA}=\widehat{KBC}\) (cmt)
⇒△BKA = △BKC (gcg)
⇒AK=CK=\(\frac{1}{2}AC\)
Xét △BAH vuông tại H và △ABK vuông tại K có:
AB chung
\(\widehat{BAH}=\widehat{ABK}\left(=60^0\right)\)
⇒△BAH =△ABK (cạnh huyền- góc nhọn)
⇒BH=AK mà AK=CK=\(\frac{1}{2}AC\)
⇒BH=\(\frac{1}{2}AC\)
b)Ta có:
\(\widehat{MBC}=180^0-\widehat{CBA}=180^0-\left(60^0+60^0\right)=180^0-120^0=60^0\)
Xét △CMB vuông tại M và △CKB vuông tại K có:
CB chung
\(\widehat{MBC}=\widehat{KBC}\left(=60^0\right)\)
⇒ △CMB =△CKB(cạnh huyền- góc nhọn)
⇒CM=CK⇒△KMC cân tại C có \(\widehat{MCK}=30^0+30^0=60^0\) nên △KMC đều (đpcm)

