Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Thay \(x=-4\) vào pt elip ta được:
\(\frac{y^2}{9}=1-\frac{16}{25}=\frac{9}{25}\Rightarrow\left[{}\begin{matrix}y=\frac{9}{5}\\y=-\frac{9}{5}\end{matrix}\right.\)
\(\Rightarrow MN=2.\frac{9}{5}=\frac{18}{5}\)

a) Ta có: a2 = 25 => a = 5 độ dài trục lớn 2a = 10
b2 = 9 => b = 3 độ dài trục nhỏ 2a = 6
c2 = a2 – b2 = 25 - 9 = 16 => c = 4
Vậy hai tiêu điểm là : F1(-4 ; 0) và F2(4 ; 0)
Tọa độ các đỉnh A1(-5; 0), A2(5; 0), B1(0; -3), B2(0; 3).
b)
4x2 + 9y2 = 1 <=> +
= 1
a2= => a =
=> độ dài trục lớn 2a = 1
b2 = => b =
=> độ dài trục nhỏ 2b =
c2 = a2 – b2
= -
=
=> c =
F1(- ; 0) và F2(
; 0)
A1(-; 0), A2(
; 0), B1(0; -
), B2(0;
).
c) Chia 2 vế của phương trình cho 36 ta được :
=> +
= 1
Từ đây suy ra: 2a = 6. 2b = 4, c =\(\sqrt{5}\)
=> F1(-\(\sqrt{5}\) ; 0) và F2(\(\sqrt{5}\) ; 0)
A1(-3; 0), A2(3; 0), B1(0; -2), B2(0; 2).

a, Phương trình chính tắc của (E) có dạng
\(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\) với 0<b<a
Ta có A(0;2) \(\in\left(E\right)\)<=>b=2
(E) có tiêu điểm F1\(\left(-\sqrt{5};0\right)\) => c=\(\sqrt{5}\)
Ta có \(a^2=b^2+c^2=4+5=9\)=>a=3
==> (E) \(\dfrac{x^2}{9}+\dfrac{y^2}{4}=1\)
b, 2a = 6; 2b = 4; 2c = \(2\sqrt{5}\)=>\(\dfrac{c}{a}=\dfrac{\sqrt{5}}{3}\)
c, S=4ab=24

Đáp án: C
4 x 2 + 9 y 2 = 36
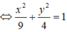
Elip có a 2 = 9 ⇒ a = 3, b 2 = 4 ⇒ b = 2
Hình chữ nhật cơ sở có hai cạnh là 2a = 6, 2b = 4. Do đó, diện tích hình chữ nhật cơ sở là: 6.4 = 24

Do trục lớn gấp đôi trục bé \(\Rightarrow2a=2\left(2b\right)\Rightarrow a=2b\Rightarrow a^2=4b^2\)
Phương trình elip có dạng:
\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\Leftrightarrow\frac{x^2}{4b^2}+\frac{y^2}{b^2}=1\)
Do \(A\left(2;-2\right)\in\left(E\right)\Rightarrow\frac{2^2}{4b^2}+\frac{\left(-2\right)^2}{b^2}=1\)
\(\Leftrightarrow\frac{1}{b^2}+\frac{4}{b^2}=1\Rightarrow\frac{5}{b^2}=1\Rightarrow b^2=5\Rightarrow a^2=4.5=20\)
Phương trình elip: \(\frac{x^2}{20}+\frac{y^2}{5}=1\)



Đáp án C