Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đường tròn c: Đường tròn qua B với tâm O Đoạn thẳng h: Đoạn thẳng [C, D] Đoạn thẳng i: Đoạn thẳng [A, B] Đoạn thẳng j: Đoạn thẳng [C, E] Đoạn thẳng k: Đoạn thẳng [D, E] Đoạn thẳng l: Đoạn thẳng [E, A] Đoạn thẳng m: Đoạn thẳng [E, B] Đoạn thẳng n: Đoạn thẳng [B, C] O = (4.35, -6.12) O = (4.35, -6.12) O = (4.35, -6.12) B = (12.58, -6.03) B = (12.58, -6.03) B = (12.58, -6.03) Điểm C: Giao điểm đường của c, g Điểm C: Giao điểm đường của c, g Điểm C: Giao điểm đường của c, g Điểm A: Giao điểm đường của c, f Điểm A: Giao điểm đường của c, f Điểm A: Giao điểm đường của c, f Điểm D: Giao điểm đường của c, g Điểm D: Giao điểm đường của c, g Điểm D: Giao điểm đường của c, g Điểm E: Điểm trên c Điểm E: Điểm trên c Điểm E: Điểm trên c Điểm M: Giao điểm đường của i, j Điểm M: Giao điểm đường của i, j Điểm M: Giao điểm đường của i, j
a) Do E thuộc đường tròn tâm O nên \(\widehat{CED}=90^o\)
Xét tứ giác MEDO có \(\widehat{MED}=\widehat{MOD}=90^o\) nên MEDO là tứ giác nội tiếp hay 4 điểm E, M, O , D cùng thuộc một đường tròn.
b) Ta có \(\widehat{AEB}=\widehat{CED}=90^o\) nên \(EA^2+EB^2=AB^2;EC^2+ED^2=CD^2\)
Vậy thì \(EA^2+EB^2+EC^2+ED^2=CD^2+AB^2=4R^2+4R^2=8R^2\)
c) Ta có ngay \(\Delta CMO\sim\Delta CDE\left(g-g\right)\Rightarrow\frac{CM}{CD}=\frac{CO}{CE}\)
Vậy thì \(CM.CE=CO.CD=R.2R=2R^2\)
d) Ta thấy \(\widehat{AOC}=\widehat{COB}=90^o\Rightarrow\widebat{AC}=\widebat{CB}\)
Vậy thì \(\widehat{AEC}=\widehat{CEB}\) (Hai góc nội tiếp cùng chắn một cung)
hay EC là phân giác góc \(\widehat{AEB}.\)
e) Ta thấy \(\widehat{MCB}=\widehat{MAE}\) (Hai góc nội tiếp cùng chắn cung EB)
Vậy nên \(\Delta MCB\sim\Delta MAE\left(g-g\right)\Rightarrow\frac{MC}{MA}=\frac{MB}{ME}\Rightarrow MA.MB=MC.ME\)

d, Vi ED la tiep tuyen (chung minh tren) => tam giac EDF vuong tai D
co \(\widehat{CDE}=\frac{1}{2}sd\widebat{DC}=\frac{1}{2}\widehat{COD}=\frac{1}{2}.120=60^o\)
ma \(\widehat{CED}+\widehat{COD}=180^o\Rightarrow\widehat{CED}=180-120=60^o\)
suy ra \(\Delta CED\) deu => EC=CD (1)
mat khac cung co \(\widehat{CFD}=\widehat{CDF}\) (phu hai goc bang nhau)
=> tam giac CDF can tai C
suy ra CD=CF (2)
tu (1),(2) suy ra dpcm

a) Xét ΔDAB có
DO là đường trung tuyến ứng với cạnh AB(O là trung điểm của AO)
DO là đường cao ứng với cạnh AB(gt)
Do đó: ΔDAB cân tại D(Định lí tam giác cân)
Suy ra: \(DA=DB\)(hai cạnh bên)
hay \(sđ\stackrel\frown{DA}=sđ\stackrel\frown{DB}\)
Xét (O) có
\(\widehat{AID}\) là góc nội tiếp chắn cung AD
\(\widehat{BID}\) là góc nội tiếp chắn cung BD
mà \(sđ\stackrel\frown{DA}=sđ\stackrel\frown{DB}\)(cmt)
nên \(\widehat{AID}=\widehat{BID}\)
hay ID là tia phân giác của \(\widehat{AIB}\)(đpcm)
b) Xét (O) có
\(\widehat{AIB}\) là góc nội tiếp chắn nửa đường tròn
nên \(\widehat{AIB}=90^0\)(Hệ quả góc nội tiếp)
hay \(\widehat{FIB}=90^0\)
Xét tứ giác BIFO có
\(\widehat{FOB}\) và \(\widehat{FIB}\) là hai góc đối
\(\widehat{FOB}+\widehat{FIB}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: BIFO là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
hay B,I,F,O cùng thuộc 1 đường tròn(đpcm)

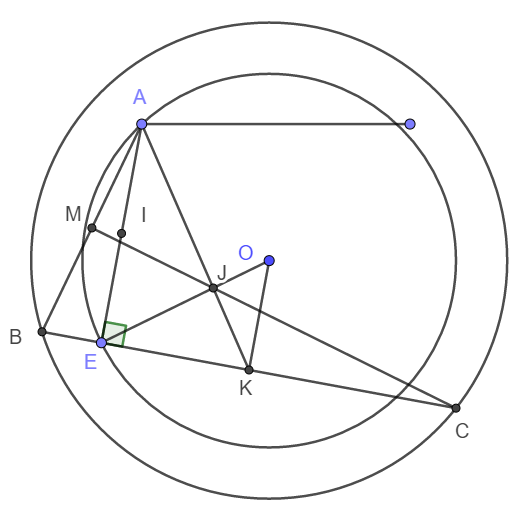
a) Gọi I, K lần lượt là trung điểm của AE và BC.
Ta có : \(EB^2=\left(BK-EK\right)^2;EC^2=\left(KC+EK\right)^2\)
\(\Rightarrow EB^2+EC^2=2\left(BK^2+EK^2\right)=2\left(BO^2-OK^2+OE^2-OK^2\right)\)
\(=2\left(R^2+r^2\right)-4OK^2\)
\(AE^2=4AI^2=4\left(r^2-OI^2\right)\)
\(\Rightarrow EB^2+EC^2+EA^2=2R^2+6r^2-4\left(OI^2+OK^2\right)\)
Mà OIEK là hình chữ nhật nên \(OI^2+OK^2=OE^2=r^2\)
\(\Rightarrow EB^2+EC^2+EA^2=2R^2+2r^2\) không đổi.
b) Giả sử EO giao với AK tại J.
Vì IOEK là hình chữ nhật nên OK song song và bằng EI. Vậy nên OK song song và bằng một nửa AE.
Do đó \(\frac{JE}{JO}=\frac{AJ}{JK}=\frac{AE}{OK}=2\)
Vì OE cố định nên J cố định; Vì AK là trung tuyến của tam giác ABC nên J là trọng tâm tam giác ABC
Suy ra J thuộc MC.
Vậy MC đi qua J cố định.
c) Vì AK = 3/2AJ nên H trùng K.
Do đó OH vuông góc BC. Suy ra H thuộc đường tròn đường kính OE.

câu c hình như bn nhầm đỉnh tứ giác thì phải
d) bn cm ED là phân giác góc AEB (giống câu a) rồi dùng t/c phân giác trog và ngoài của tg AEB nhé

bạn tự vẽ hình nha
bạn dễ dàng chứng minh đc tam giác ACO là tam giác đều ( AM = MO ; CM vuong goc vs AO )
trong tam giác ECO có EA = AO = AC nên suy ra tam giac ECO vuong tai C
suy ra EC vuong goc vs OC . (dpcm )
b, sử dụng định lí pitago

a: Xét tứ giác ODAE có
góc ODA+góc OEA=180 độ
=>ODAE là tứ giác nội tiếp
b: \(AE=\sqrt{\left(3R\right)^2-R^2}=2\sqrt{2}\cdot R\)
\(OI=\dfrac{OE^2}{OA}=\dfrac{R^2}{3R}=\dfrac{R}{3}\)
c: Xét ΔDIK vuông tại I và ΔDHE vuông tại H có
góc IDK chung
=>ΔDIK đồng dạng vơi ΔDHE
=>DI/DH=DK/DE
=>DH*DK=DI*DE=2*IE^2
Bạn ơi mình chưa học góc nội tiếp chắn nửa đâu