Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C E F M
\(\Delta ABM\) vuông tại \(A\Rightarrow AB< BM\)
Do đó: \(AB< BE+ME\) __(1)__
Và \(AB< BF-MF\) __(2)__
\(\Delta MAE=\Delta MCF\) ( cạnh huyền - góc nhọn )
\(\Rightarrow ME=MF\) __(3)__
Từ (1),(2),(3) suy ra:
\(AB+AB< BE+BF\)
Do đó
\(2AB< BE+BF\) nên \(AB< \dfrac{BE+BF}{2}\)

a: Xét ΔMEA vuông tại E và ΔMFC vuông tại F có
MA=MC
góc AME=góc CMF
=>ΔMEA=ΔMFC
=>ME=MF
b: BE+BF
=BE+BE+EF
=BE+BE+2*ME
=2*BE+2*ME
=2*BM
c: ΔAMB vuông tại A
=>AB<BM

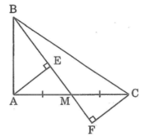
Trong ΔABM, ta có ∠(BAM) = 90o
Suy ra: AB < BM (trong tam giác vuông cạnh huyền lớn nhất)
Mà BM = BE + EM = BF - MF
Suy ra: AB < BE + EM
AB < BF - FM
Suy ra:AB + AB < BE + ME + BF - MF (1)
Xét hai tam giác vuông AEM và CFM, ta có:
∠(AEM) = ∠(CFM) = 90o
AM = CM (gt)
∠(AME) = ∠(CMF) (đối đỉnh)
Suy ra: ΔAEM = ΔCFM (cạnh huyền - góc nhọn)
Suy ra: ME = MF (2)
Từ (1) và (2) suy ra: AB + AB < BE + BF
Suy ra: 2AB < BE + BF
Vậy AB < (BE + BF) / 2 .

a, Xét △MEA vuông tại E và △MFC vuông tại F
Có: MA = MC (gt)
EMA = FMC (2 góc đối đỉnh)
=> △MEA = △MFC (ch-gn)
=> ME = MF (2 cạnh tương ứng)
b, Ta có: BE = BM - ME và BF = BM + MF
=> BE + BF = BM - ME + BM + MF
=> BE + BF = (BM + BM) - (ME - MF)
=> BE + BF= 2BM
c, Xét △ABM vuông tại A có: AB < BM (quan hệ cạnh)
d, Ta có: BE + BF = 2BM
=> (BE + BF) : 2 = BM
Lại có: AB < BM (cmt)
=> AB < (BE + BF) : 2
Bn ơi vào phần CHTT ý,có nhiều lm
A B C E M F
ZXVXCVXCVV
XÉT TAM GIÁC ABM :Â=90o
=>BM>AB
=>BE+EM>AB(1)
HAY BF-MF>AB(2)
AME=CFM(CH-GN)
=>EM=MF(3)
TỪ 1 2 3 => 2AB< BE+BF
=>\(AB< \frac{BE+BF}{2}\)