Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
a.\(\left(x+y\right)^2-\left(x-y\right)^2=\left(x+y-x+y\right)\left(x+y+x-y\right)=2\left(x+y\right)\)
b.\(2\left(x+y\right)\left(x-y\right)+\left(x+y\right)^2+\left(x-y\right)^2=\left(x+y+x-y\right)^2=4x^2\)

\(A=\left(\frac{21}{x^2-9}-\frac{x-4}{3-x}-\frac{x-1}{3+x}\right)\div\left(1-\frac{1}{x+3}\right)\)
\(=\left(\frac{21}{\left(x-3\right)\left(x+3\right)}+\frac{\left(x-4\right)\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}-\frac{\left(x-1\right)\left(x-3\right)}{\left(x-3\right)\left(x+3\right)}\right)\div\left(\frac{x+3}{x+3}-\frac{1}{x+3}\right)\)
\(=\left(\frac{21}{\left(x-3\right)\left(x+3\right)}+\frac{x^2-x-12}{\left(x-3\right)\left(x+3\right)}-\frac{x^2-4x+3}{\left(x-3\right)\left(x+3\right)}\right)\div\frac{x+2}{x+3}\)
\(=\frac{21+x^2-x-12-x^2+4x-3}{\left(x-3\right)\left(x+3\right)}\times\frac{x+3}{x+2}\)
\(=\frac{3x+6}{x-3}\times\frac{1}{x+2}=\frac{3\left(x+2\right)}{\left(x-3\right)\left(x+2\right)}=\frac{3}{x-3}\)
\(A=\left(\frac{21}{x^2-9}-\frac{x-4}{3-x}-\frac{x-1}{3+x}\right):\left(1-\frac{1}{x+3}\right)\)
\(=\left(\frac{21}{x^2-9}+\frac{x-4}{x-3}-\frac{x-1}{x+3}\right):\left(\frac{x+2}{x+3}\right)\)
\(=\left(\frac{21}{\left(x-3\right)\left(x+3\right)}+\frac{\left(x-4\right)\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}-\frac{\left(x-1\right)\left(x-3\right)}{\left(x-3\right)\left(x+3\right)}\right):\left(\frac{x+2}{x+3}\right)\)
\(=\left(\frac{21+x^2-x-12-x^2+4x-3}{\left(x-3\right)\left(x+3\right)}\right):\left(\frac{x+2}{x+3}\right)\)
\(=\frac{6+3x}{\left(x-3\right)\left(x+3\right)}.\frac{x+3}{x+2}=\frac{3\left(x+2\right)\left(x+3\right)}{\left(x-3\right)\left(x+3\right)\left(x+2\right)}=\frac{3}{x-3}\)

- \(B=\left(\frac{21}{\left(x-3\right)\left(x+3\right)}+\frac{\left(x-4\right)\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}-\frac{\left(x-3\right)\left(x-1\right)}{\left(x-3\right)\left(x+3\right)}\right):\frac{x+3-1}{x+3}\)\(=\frac{3x+6}{\left(x-3\right)\left(x+3\right)}.\frac{x+3}{x+2}=\frac{3\left(x+2\right)\left(x+3\right)}{\left(x-3\right)\left(x+3\right)\left(x+2\right)}=\frac{3}{x-3}\)
- Điều kiện \(x\ne3\) \(\Rightarrow\frac{-3}{5}=\frac{3}{x-3}\Leftrightarrow x-3=-5\Leftrightarrow x=-2\)
- \(B=\frac{3}{x-3}< 0\Leftrightarrow x-3< 0\Leftrightarrow x< 3\)
a) B=(\(\frac{21}{x^2-9}\)-\(\frac{x-4}{3-x}\)-\(\frac{x-1}{3+x}\)) : (1-\(\frac{1}{x+3}\)) (ĐK: x khác +-3)
=(\(\frac{21}{\left(x-3\right).\left(x+3\right)}\)+\(\frac{x-4}{x-3}\)-\(\frac{x-1}{x+3}\)) : (1-\(\frac{1}{x+3}\))
=(\(\frac{21+\left(x+4\right).\left(x+3\right)-\left(x-1\right).\left(x-3\right)}{\left(x-3\right).\left(x+3\right)}\):(\(\frac{x+3-1}{x+3}\))
=(\(\frac{3x+6}{\left(x-3\right).\left(x+3\right)}\)) . (\(\frac{x+3}{x+2}\))
=(\(\frac{3.\left(x+2\right)}{\left(x-3\right).\left(x+3\right)}\). \(\frac{x+3}{x+2}\)
=\(\frac{3}{x-3}\)
b) B=\(\frac{3}{x-3}\)=\(\frac{-3}{5}\)
(=) \(\frac{3.5}{x-3}\)=-3
(=) -3.(x-3) = 15
(=) -3x=6
(=) x=-2
vậy x=2 thì B=\(\frac{-3}{5}\)
c) B=\(\frac{3}{x-3}\)<0
(=) 3 < x - 3
(=) -x < - 3 - 3
(=) x > 6
Vậy với x > 6 thì B < 0

\(B=\left(\frac{21}{x^2-9}-\frac{x-4}{3-x}+\frac{x-1}{3+x}\right)\div\left(1-\frac{1}{x+3}\right)\)
\(B=\left(\frac{21}{x^2-9}+\frac{x-4}{x-3}+\frac{x-1}{x+3}\right)\div\left(\frac{x+3}{x+3}-\frac{1}{x+3}\right)\)
\(B=\left(\frac{21}{\left(x+3\right)\left(x-3\right)}+\frac{\left(x-4\right)\left(x+3\right)}{\left(x+3\right)\left(x-3\right)}+\frac{\left(x-1\right)\left(x-3\right)}{\left(x+3\right)\left(x-3\right)}\right)\div\frac{x+2}{x+3}\)
\(B=\left(\frac{21}{\left(x+3\right)\left(x-3\right)}+\frac{x^2-x-12}{\left(x+3\right)\left(x-3\right)}+\frac{x^2-4x+3}{\left(x+3\right)\left(x-3\right)}\right)\cdot\frac{x+3}{x+2}\)
\(B=\left(\frac{21+x^2-x-12+x^2-4x+3}{\left(x+3\right)\left(x-3\right)}\right)\cdot\frac{x+3}{x+2}\)
\(B=\frac{2x^2-5x+12}{\left(x+3\right)\left(x-3\right)}\cdot\frac{x+3}{\left(x+2\right)}\)
\(B=\frac{2x^2-5x+12}{\left(x-3\right)\left(x+2\right)}\)
\(B=\frac{2x^2-5x+12}{x^2-x-6}\)
Đến đây là chịu ạ :(

a) \(\left(x^2-1\right)^3-\left(x^4+x^2+1\right)\left(x^2-1\right)=\left(x^2-1\right)\left[\left(x^2-1\right)^2-\left(x^4+x^2+1\right)\right]\)
\(=\left(x^2-1\right)\left(x^4-2x^2+1-x^4-x^2-1\right)=\left(x^2-1\right)\left(-3x^2\right)\)
\(=-3x^4+3x^2=3\left(x^2-x^4\right)=3\left(x-x^2\right)\left(x+x^2\right)=\left(3x-3x^2\right)\left(x+x^2\right).\)
b)\(\left(x^4-3x^2+9\right)\left(x^2+3-\left(3+x^2\right)\right)^3=\left(x^4-3x^2+9\right).0^3=0\)
c)\(\left(x-3\right)^3-\left(x-3\right)\left(x^2+3x+9\right)+6\left(x+1\right)^2=\left(x-3\right)^3-\left(x^3-3^3\right)+6\left(x^2+2x+1\right)\)
\(=\left(x-3\right)^3-\left[\left(x-3\right)^3+3.x.3.\left(x-3\right)\right]+6x^2+12x+6\)
\(=6x^2+12x+6-9x\left(x-3\right)=6x^2+12x+6-9x^2+27x\)
\(=39x-3x^2+6=3\left(13x-x^2+2\right).\)

\(B=\left(\frac{21}{x^2-9}+\frac{\left(x-4\right)\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}+\frac{\left(x-1\right)\left(x-3\right)}{\left(x-3\right)\left(x+3\right)}\right):\frac{x+2}{x+3}\)
\(B=\frac{2x^2-5x+12}{x^2-9}\cdot\frac{x+3}{x+2}\)
\(B=\frac{2x^2-5x-12}{\left(x-3\right)\left(x+2\right)}\)
\(B=\frac{2x^2-5x+12}{x^2-x-6}\)
Thik thì tách tiếp nha
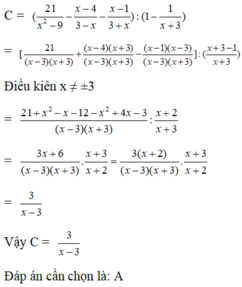
\(C=\dfrac{21+\left(x^2-x-12\right)-x^2+4x-3}{\left(x-3\right)\left(x+3\right)}:\dfrac{x+3-1}{x+3}\)
\(=\dfrac{3x+6}{x-3}\cdot\dfrac{1}{x+2}=\dfrac{3}{x-3}\)