Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.Dấu hiệu là số học sinh nam trong từng lớp
2 . Ta có
c = b + 2
a = b - 2
và a + b +c = 66 <=> b - 2 + b + b + 2 = 66
=> 3b = 66
=> b = 66 : 3 = 22
=> a = 22 - 2 = 20
=> c = 22 + 2 = 24
| Giá trị (x) | 19 | 20 | 21 | 22 | 23 | 24 |
| Tần số (n) | 2 | 7 | 3 | 4 | 3 | 1 |
Bổ sung thêm ở bảng tần số là N = 20
- Có 20 lớp học được điều tra .
- Có 7 lớp có 20 bạn nam.
- Có 2 lớp có 19 ban nam.
- Có 1 lớp có 24 bạn nam.
- Số bạn nam khoảng từ 19 - 24.
\(\overline{X}=\frac{19.2+20.7+21.3+22.4+23.3+24.1}{20}\)
\(\overline{X}=\frac{38+140+63+88+69+24}{20}\)
\(\overline{X}=\frac{422}{20}=21,1\approx22\)
\(Mo=20\)
b/ vì a, b, c là 3 số chẵn tự nhiên liên tiếp
=> b-c=2 => b=a+2 (1)
c-d =2 => c=b+2 (2)
thay (1) vào (2) ta có c= a+2+2
c= a+4
có a +b +c = 66
=> a + a+2+a+4 = 66
=>3a + 6 =66
=>3a + 6 = 66
=> 3a = 60
=> a =20 (t/m)
b = a + 2= 20 + 2 = 22
c = a + 4 = 20 + 4 = 24

Answer:
Bài 1:
Ta có:
\(1.9=\left(-2\right).\left(-4\right)=1,6.5=0,5.16=10.0,8=8\)
Hay: \(x_1.y_1=x_2.y_2=x_3.y_3=x_4.y_4=x_5.y_5=8\)
Vậy x tỉ lệ nghịch với y
Bài 2:
Vì hai đại lượng x và y tỉ lệ nghịch với nhau nên ta có: \(x.y=a\Rightarrow a=x_1.y_1=2.30=60\)
Vậy \(a=60\)
Ta có công thức: \(y=\frac{60}{x}\)
Với a = 60 \(\Rightarrow y=\frac{60}{x}\)
\(?1=\frac{60}{x_2}=\frac{60}{3}=20\)
\(?2=\frac{60}{x_3}=\frac{60}{4}=15\)
\(?3=\frac{60}{x_4}=\frac{60}{5}=12\)

Trả lời:
Hình C bn nhé
Đây ko phải toán lớp 7 đâu bạn
Mk nghĩ đây toán lớp 4

Vì x và y là hai đại lượng tỉ lệ nghịch nên: a = xy = -2. (-15) = 30
Ta có kết quả sau:
|
x |
-2 |
-1 |
1 |
2 |
3 |
5 |
|
y |
-15 |
-30 |
30 |
15 |
10 |
6 |
Vì x và y là hai đại lượng tỉ lệ nghịch nên: a = xy = -2. (-15) = 30
Ta có kết quả sau:
|
x |
-2 |
-1 |
1 |
2 |
3 |
5 |
|
y |
-15 |
-30 |
30 |
15 |
10 |
6 |

Vì mỗi giá trị của x ta xác định được chỉ một giá trị của y tương ứng nên đại lượng y là hàm số của đại lượng x
Vì mỗi giá trị của x ta xác định được chỉ một giá trị tương ứng của y nên đại lượng y là hàm số của đại lượng x.

a) Vì x và y là hai đại lượng tỉ lệ nghịch nên xy = a
Khi \(x=2;y=15\Rightarrow a=xy=2.15=30\Rightarrow y=\dfrac{30}{x}\)
Kết quả như sau:
|
x |
x1 = 2 |
x2 = 3 |
x3 = 5 |
x4 = 6 |
|
y |
y1 = 15 |
y2 = 10 |
y3 = 6 |
y4 = 5 |
|
xy |
x1y1 = 30 |
x2y2 = 30 |
x3y3 = 30 |
x4y4 = 30 |
b) \(x_1y_1=x_2y_2=x_3y_3=x_4y_4=30\)

Từ cột thứ 6 ta tính được hệ số a từ công thức y = 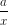 ;
;
a = 4.1,5 = 6.Từ đó tính được các số còn lại. Ta được bảng sau:
![]()

a) Tất cả các cặp giá trị tương ứng (x;y) là: (0;0), (1;2); (2; 4); (3; 6); (4; 8).
b) Trên hình vẽ 0, A, B, C, D là vị trí của các điểm biểu diễn các cặp giá trị tương ứng của x và y trong câu a.
a) Tất cả các cặp giá trị tương ứng (x;y) là: (0;0), (1;2); (2; 4); (3; 6); (4; 8).
b) Trên hình vẽ 0, A, B, C, D là vị trí của các điểm biểu diễn các cặp giá trị tương ứng của x và y trong câu a.


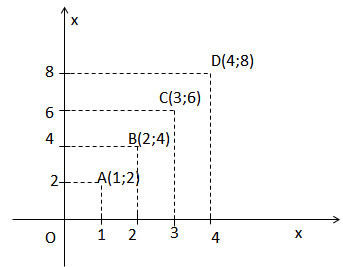
a) Điền số thích hợp vào ô trống:
b) Hai đại lượng s và t tỉ lệ thuận vì s =12t, hệ số tỉ lệ bằng 12.




a) Tỉ lệ của y đối với x là : \(\dfrac{{{y_1}}}{{{x_1}}} = 5\)
\( \Rightarrow \) Hệ số tỉ lệ của y đối với x là : \(5\)
b) Dựa vào hệ số tỉ lệ của y đối với x vừa tính được
Xét \({y_2} =5. {x_2}=5.2=10\)
Xét \({y_2} =5. {x_3}=5.6= 30\)
Xét \({y_4} = 5.{x_4}=5.100= 500\)
c) Ta có: \(\dfrac{{{y_1}}}{{{x_1}}},\dfrac{{{y_2}}}{{{x_2}}},\dfrac{{{y_3}}}{{{x_3}}},\dfrac{{{y_4}}}{{{x_4}}}\) lần lượt bằng : \(\dfrac{5}{1},\dfrac{{10}}{2},\dfrac{{30}}{6},\dfrac{{500}}{{100}}\)
Các tỉ số giữa y và x tương ứng đều bằng nhau (cùng = 5)