Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Vì đường tròn (O) và (O') tiếp xúc ngoài tại A nên O, A và O’ thẳng hàng.
Ta có: MB = MC (M là TĐ của BC)
Xét (O) ta có: DE vg góc BC (gt)
mà M là TĐ của BC
Suy ra : M là TĐ của DE ( đường kính vuông góc với dây cung)
Xét TG BDCE có 2 đường chéo DE và BC cắt nhau tại trung điểm M của mỗi đường
Suy ra: BDCE là hình bình hành.
(Bổ sung)
Lại có: BC ⊥ DE
Suy ra tứ giác BDCE là hình thoi

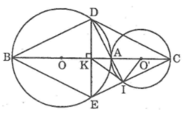
Vì đường tròn (O) và (O’) tiếp xúc ngoài tại A nên O, A và O’ thẳng hàng
Ta có: KB = KC (gt)
Trong đường tròn (O) ta có:
AB ⊥ DE tại K
Suy ra: KD = KE (đường kính vuông góc với dây cung)
Tứ giác BDCE có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên nó là hình bình hành.
Lại có: BC ⊥ DE
Suy ra tứ giác BDCE là hình thoi.


a: Ta có: ΔODE cân tại O
mà OM là đường cao
nên Mlà trung điểm của DE
Xét tứ giác BDCE có
M là trung điểm chung của BC và DE
BC vuông góc với DE
Do đo: BDCE là hình thoi
b: Xét (O') có
ΔAFC nội tiếp
AC là đường kính
Do đo: ΔAFC vuông tại F
=>FC vuông góc với FA
=>FA vuông góc với BD
Xét (O) có
ΔADB nội tiếp
AB là đường kính
Do đo: ΔADB vuông tại D
=>DA vuông góc với BD
=>D,A,F thẳng hàng