Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

đăng từng câu 1 thôi, nhiều nhất là 3 câu/ 1 lần hỏi vì đâu có giới hạn số lần hỏi

Ta khai triển VT trước
\(VT=\frac{1-b-c+bc}{b+c}+\frac{1-c-a+ca}{c+a}+\frac{1-a-b+ab}{a+b}=\frac{\left(1-b\right)-c\left(1-b\right)}{1-a}+\frac{\left(1-c\right)-a\left(1-c\right)}{1-b}+\frac{\left(1-a\right)-b\left(1-a\right)}{1-c}=\frac{\left(1-c\right)\left(1-b\right)}{1-a}+\frac{\left(1-c\right)\left(1-a\right)}{1-b}+\frac{\left(1-a\right)\left(1-b\right)}{1-c}\)Với a,b,c luôn dương vào a+b+c=1 nên a,b,c<1\(\Rightarrow\)1-a,1-b,1-c>0
Áp dụng Cosi có \(\frac{\left(1-c\right)\left(1-b\right)}{1-a}+\frac{\left(1-c\right)\left(1-a\right)}{1-b}\ge2\left(1-c\right)\left(1\right)\).Tương tự: \(\frac{\left(1-c\right)\left(1-a\right)}{1-b}+\frac{\left(1-a\right)\left(1-b\right)}{1-c}\ge2\left(1-a\right)\left(2\right)\)
\(\frac{\left(1-c\right)\left(1-b\right)}{1-a}+\frac{\left(1-a\right)\left(1-b\right)}{1-c}\ge2\left(1-b\right)\left(3\right)\)
Cộng (1),(2) và (3) có \(2VT\ge2\left(3-a-b-c\right)\Leftrightarrow VT\ge3-1=2\)

\(M=\frac{1}{ab}+\frac{1}{a^2+ab}+\frac{1}{b^2+ab}+\frac{1}{a^2+b^2}\)
\(=\left(\frac{1}{2ab}+\frac{1}{a^2+b^2}\right)+\left(\frac{1}{a^2+ab}+\frac{1}{b^2+ab}\right)+\frac{1}{2ab}\)
\(\ge\frac{\left(1+1\right)^2}{a^2+2ab+b^2}+\frac{\left(1+1\right)^2}{a^2+ab+b^2+ab}+\frac{2}{\left(a+b\right)^2}\)
\(=\frac{4}{\left(a+b\right)^2}+\frac{4}{\left(a+b\right)^2}+\frac{2}{\left(a+b\right)^2}\)
\(\ge\frac{4}{1}+\frac{4}{1}+\frac{2}{1}=10\)
Dấu = xảy ra khi a = b = \(\frac{1}{2}\)


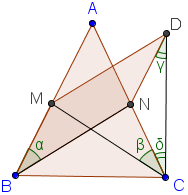
gọi 2 đường phân giác trong BN, CM bằng nhau
dựng hình bình hành BMDN và kí hiệu các góc α,β,γ,δα,β,γ,δ như hình vẽ
tam giác CMD cân tại M nên α+γ=β+δα+γ=β+δ (1)
nếu α>βα>β thì xét hai tam giác BCN và CBM có BC chung, BN=CM,CBNˆ>BCMˆ⇒CN>BMBN=CM,CBN^>BCM^⇒CN>BM
mà BM=ND⇒γ>δ⇒α+γ>β+δBM=ND⇒γ>δ⇒α+γ>β+δ, mâu thuẫn với (1)
tương tự, ko thể xảy ra trường hợp α<βα<β
suy ra α=βα=β, đpcm
a)
\(\left(a-b\right)^2\ge0\Rightarrow a^2+b^2\ge2ab\forall a,b\) {cơ bản nhất, cần thiết nhất}
\(\Rightarrow a^2+b^2\ge ab\) đẳng thức khi a=b=0
b)Nhân 2 hai vế chuyển hết về VT
\(\Leftrightarrow\left(a^2-2ab+b^2\right)+\left(a^2-2a+1\right)+\left(a^2-2b+1\right)\ge0\)
\(\Leftrightarrow\left(a-b\right)^2+\left(a-1\right)^2+\left(b-1\right)^2\ge0\)
Hiển nhiên tổng 3 số không âm => không âm
đẳng thức khi \(\left\{{}\begin{matrix}a-b=0\\a=1\\b=1\end{matrix}\right.\) \(\Rightarrow a=b=1\)