Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Chứng minh được tương tự câu 1a,
=> O ' M O ^ = 90 0
Áp dụng hệ thức lượng trong tam giác vuông tính được MA = R r
b, Chứng minh
S
B
C
O
O
'
=
R
+
r
R
r
c, Chứng minh được: ∆BAC:∆OMO’ => S B A C S O M O ' = B C O O ' 2
=> S B A C = S O M O ' . B C 2 O O ' 2 = 4 R r R r R + r
d, Tứ giác OBCO’ là hình thang vuông tại B và C có IM là đường trung bình => IM ⊥ BC = {M}


a, Chứng minh được B A C ^ = 90 0 kết hợp B A D ^ = C A E ^ = 90 0 => ĐPCM
b, Chứng minh ∆BAD:∆EAC => AD.AE=AB.AC(đpcm)
c, Chứng minh tứ giác OIO’K là hình chữ nhật
Đường tròn ngoại tiếp ∆OKO’ chính là đường tròn ngoại tiếp hình chữ nhật ,có đường kính là IK mà IK ⊥ BC tại I

a: Xét (O) có
ID,IA là các tiếp tuyến
Do đó: IO là phân giác của góc DIA
=>\(\widehat{DIA}=2\cdot\widehat{OIA}\)
Xét (O') có
IA,IE là các tiếp tuyến
Do đó: IO' là phân giác của góc AIE
=>\(\widehat{AIE}=2\cdot\widehat{AIO'}\)
Ta có: \(\widehat{DIA}+\widehat{EIA}=180^0\)(hai góc kề bù)
=>\(2\left(\widehat{OIA}+\widehat{O'IA}\right)=180^0\)
=>\(2\cdot\widehat{OIO'}=180^0\)
=>\(\widehat{OIO'}=90^0\)
b: Xét (O) có
ID,IA là các tiếp tuyến
Do đó: ID=IA
Xét (O') có
IA,IE là các tiếp tuyến
Do đó: IA=IE
Ta có: IA=IE
ID=IA
Do đó: ID=IE
=>I là trung điểm của DE
=>I là tâm đường tròn đường kính DE
Xét ΔDAE có
AI là bán kính
\(AI=\dfrac{DE}{2}\)
Do đó: ΔADE vuông tại A
=>A nằm trên (I)
Xét (I) có
IA là bán kính
O'O\(\perp\)IA tại A
Do đó: OO' là tiếp tuyến của (I)
=>O'O là tiếp tuyến của đường tròn đường kính DE

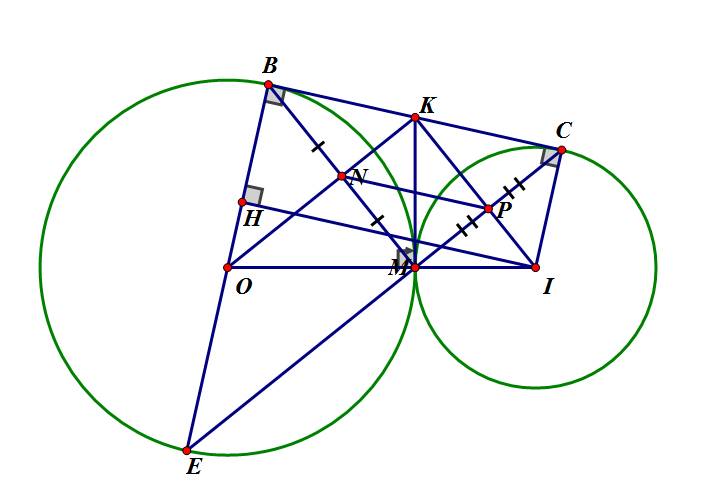
a) Trong (O) có: KB,KM là hai tiếp tuyến cắt nhau tại K.
\(\Rightarrow KB=KM\left(1\right)\).
Trong (I) có: KC,KM là hai tiếp tuyến cắt nhau tại K.
\(\Rightarrow KC=KM\left(2\right)\)
\(\left(1\right),\left(2\right)\Rightarrow KB=KC\)
△BME nội tiếp đường tròn (O) đường kính BE.
⇒△BME vuông tại MM.
\(\Rightarrow\widehat{BME}=90^0\)
b) Ta có: K thuộc đường trung trực của BM (\(KB=KM\))
O thuộc đường trung trực của BM \(\left(OB=OM\right)\)
⇒OK là đường trung trực của BM mà OK cắt BM tại N.
⇒N là trung điểm BM.
- Ta có: K thuộc đường trung trực của CM (\(KC=KM\))
I thuộc đường trung trực của CM \(\left(IC=IM\right)\)
⇒IK là đường trung trực của CM mà IK cắt CM tại P.
⇒P là trung điểm IK và \(CM\perp IK\) tại P.
Xét △BCM có: N là trung điểm BM, P là trung điểm CM.
⇒NP là đường trung bình của △BCM.
⇒NP//CM.
c) *Hạ \(IH\perp OB\) tại H.
Xét tứ giác BCIH có: \(\widehat{HBC}=\widehat{BCI}=\widehat{BHI}=90^0\)
⇒BCIH là hình chữ nhật.
\(\Rightarrow BC=IH;IC=BH=r\)
Xét △ICK vuông tại C có IP là đường cao:
\(\Rightarrow IK.IP=IC^2=r^2\)
Xét △OHI vuông tại H có:
\(HI^2+OH^2=OI^2\)
\(\Rightarrow HI=\sqrt{OI^2-OH^2}=\sqrt{\left(r+R\right)^2-\left(r-R\right)^2}=\sqrt{4Rr}=2\sqrt{Rr}\)
Mà \(BC=HI\Rightarrow BC=2\sqrt{Rr}\left(1'\right)\)
Ta có: \(2\sqrt{IM.IO-IK.IP}=2\sqrt{r\left(r+R\right)-r^2}=2\sqrt{Rr}\left(2'\right)\)
\(\left(1'\right),\left(2'\right)\Rightarrow BC=2\sqrt{IM.IO-IK.IP}\)

a, Chứng minh tứ giác AEIF là hình chữ nhật và K là trung điểm AI
b, Có IE.IO = I B 2 = B C 2 4 và IF.IO' = I C 2 = B C 2 4
=> 2.(IE.IO+IF.IO') = A B 2 + A C 2
c, PK Là đường trung bình của ∆OAI và là trung trực của EA
Ta có ∆PEK = ∆PAK nên P E K ^ = P A K ^
Vậy P E K ^ = 90 0 => đpcm
d, ∆ABC:∆IOO’ => S A B C S I O O ' = B C O O ' 2 => S A B C = S I O O ' . B C 2 O O ' 2
mà BC = 2AI'; OO' = 2a; S O I O ' = 1 2 . 2 a . I A = a . I A => S A B C = I A 2 a
I A 2 = R R ' ⩽ R + R ' 2 2 = a 2 => IA lớn nhất bằng a khi R=R’

https://diendantoanhoc.net/index.php?app=core&module=attach§ion=attach&attach_id=20602
Vào link này xem nhé
Học tốt!!!!!!!
