K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
LL
0
2D
Mn giải giúp mình với mình cần gấp lắm hôm nay mình pgair nộp rồi
3
14 tháng 10 2021
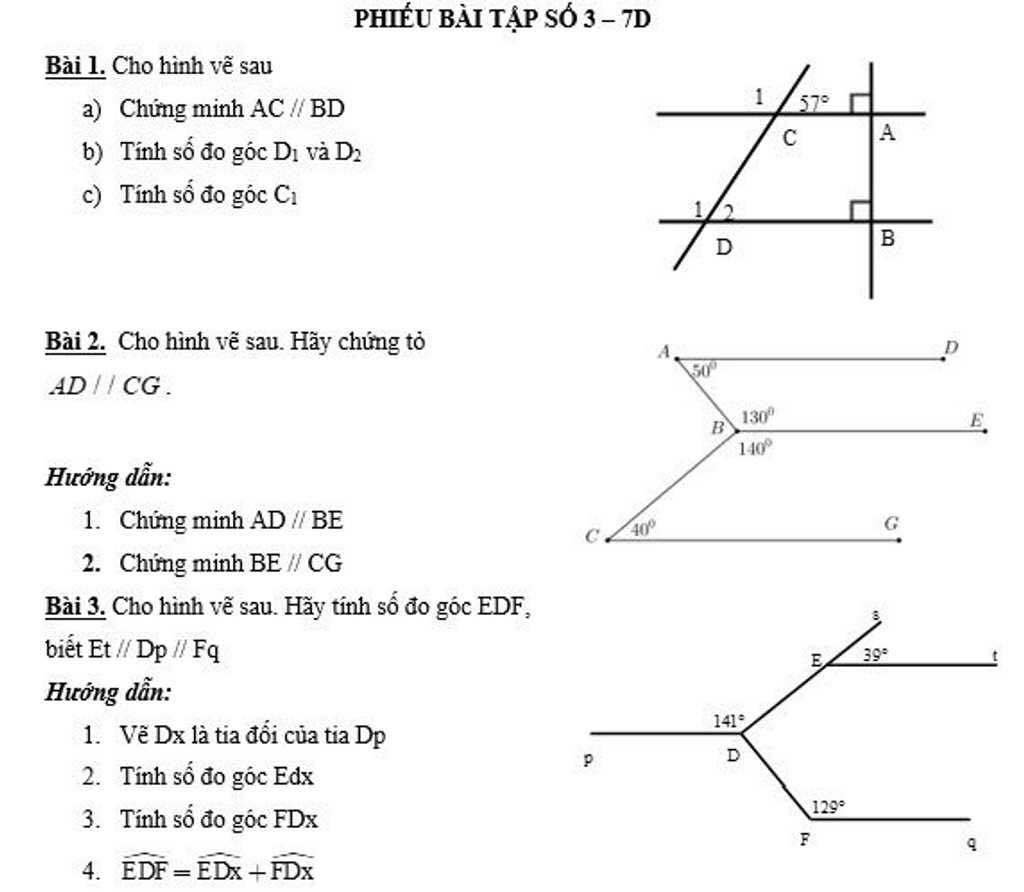
\(1,\\ a,\left\{{}\begin{matrix}AC\perp AB\\BD\perp AB\end{matrix}\right.\Rightarrow AC//BD\\ b,AC//BD\Rightarrow\widehat{D_2}=\widehat{C_1}=57^0\left(đồng.vị\right)\\ \widehat{D_2}+\widehat{D_1}=180^0\left(kề.bù\right)\Rightarrow\widehat{D_1}=180^0-57^0=123^0\\ c,AC//BD\Rightarrow\widehat{D_1}=\widehat{C_1}=123^0\left(đồng.vị\right)\)
14 tháng 10 2021
\(2,\\ \widehat{DAB}+\widehat{ABE}=50^0+130^0=180^0\)
Mà 2 góc này ở vị trí TCP nên AD//BE (1)
\(\widehat{EBC}+\widehat{BCG}=140^0+40^0=180^0\)
Mà 2 góc này ở vị trí TCP nên BE//CG (2)
Từ (1)(2) ta được AD//CG
DC
0
DC
0
LN
27 tháng 2 2018
Ta có: \(\frac{x-y}{3}=\frac{x+y}{13}=\frac{x-y+x+y}{16}=\frac{2x}{16}=\frac{x}{8}=\frac{25x}{200}=\frac{xy}{200}\)
Suy ra: \(25x=xy\Rightarrow y=25\)
Ta có: \(\frac{x-y}{3}=\frac{x+y}{13}\)
Suy ra: \(13x-13y=3x+3y\)
Thế y vào đẳng thức trên:
\(13x-325=3x+75\)
Suy ra: \(10x=325+75=400\Rightarrow x=40\)
Vậy ........
13 tháng 3 2020
Ta có:
\(\frac{x+y}{3}=\frac{5-z}{1}=\frac{y+z}{2}=\frac{9+y}{5}=k\left(1\right)\)
\(\frac{\left(x+y\right)+\left(5-z\right)+\left(y+z\right)+\left(9+y\right)}{3+1+2+5}=\frac{x+y-4}{1}\)
=> \(\hept{\begin{cases}x+y-4=k\\x+y=3k\end{cases}}\)=> \(k+4=x+y\)
=> \(4+k=3k\Rightarrow4=2k\Rightarrow k=2\)
=> \(5-z=k\Rightarrow z=5-k=5-2=3\)
\(9+y=5k\Rightarrow y=5k-9=10-9=1\)
\(x+y=3k\Rightarrow x=3k-y=6-1=5\)
Từ (1) => \(\hept{\begin{cases}x=5\\y=1\\z=3\end{cases}}\)
LH
13 tháng 3 2020
\(\frac{x+y}{5-z}=\frac{3}{1}\Leftrightarrow x+y=15-3z\) (1)
\(\frac{5-z}{y+z}=\frac{1}{2}\Leftrightarrow10-2z=y+z\Leftrightarrow y=10-3z\) (2)
\(\frac{y+z}{y+9}=\frac{2}{5}\Leftrightarrow5y+5z=2y+18\Leftrightarrow3y=18-5z\) (3)
Tù (2) và (3), ta có HPT: \(\hept{\begin{cases}y=10-3z\\3y=18-5z\end{cases}}\)<=> \(\hept{\begin{cases}y+3z=10\\3y+5z=18\end{cases}}\)
Giải HPT đó, ta có: \(y=1\), \(z=3\)
Thay \(y=1\) và \(z=3\) vào PT(1), ta có: \(x=15-3\cdot3-1=15-9-1=5\)
Vậy \(x=5\), \(y=1\) và \(z=3\).
Q
1 tháng 9 2021
Tham Khảoa pig in a poke idiom alien blind foreign god God only knows idiom hidden lesser-known moodily moodiness moody murky/uncharted waters idiom not be in sb's vocabulary idiom obscure obscurely obscurity outside pig rando random shadowy strange strangeness TBD terra incognita the outside world idiom uncharted uncommon undefined unexplored unfamiliar unheard-of unknown unknown quantity unrecorded unsung untried unused vocabulary water wild card
6
9 tháng 12 2019
=>2013= |x-4+10-x+x+101+999-x+x+1000|
rồi cộng lại đc bn + x
rồi chia Th ra
9 tháng 12 2019
Xét VP = \(\left(\left|x-4\right|+\left|x+999\right|\right)+\left(\left|x-10\right|+\left|x+1000\right|\right)+\left|x+101\right|\)
\(\ge\left|x+999+4-x\right|+\left|x+1000+10-x\right|+\left|x+101\right|\)
\(=2013+\left|x+101\right|\ge2013=VT\)
=> VP \(\ge\)VT
Dấu "=" xảy ra <=>\(\hept{\begin{cases}\left(x+999\right)\left(4-x\right)\ge0\\\left(x+1000\right)\left(10-x\right)\ge0\\x+101=0\end{cases}}\)<=> x = -101
Vậy VP = VT <=> x = -101
CC
16 tháng 12 2019
\(\left(x-7\right)^{10}-\left(x-7\right)^{x+11}=0\)\(\Leftrightarrow\left(x-7\right)^{10}\left[1-\left(x-7\right)^{x+1}\right]=0\)
\(\Leftrightarrow\orbr{\begin{cases}\left(x-7\right)^{10}=0\\1-\left(x-7\right)^{x+1}=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=7\\\left(x-7\right)^{x+1}=1\end{cases}}\)
Xét \(\left(x-7\right)^{x+1}=1\)ta có:
TH1: \(x+1=0\)và \(x-7\inℤ\)\(\Rightarrow x=-1\left(tm\right)\)
TH2: \(x-7=-1\)và \(x+1\)là số dương chẵn \(\Rightarrow x=6\left(tm\right)\)
TH3: \(x-7=1\)và \(x+1\inℕ^∗\) \(\Rightarrow x=8\left(tm\right)\)
Vậy \(x\in\left\{-1;6;7;8\right\}\)
Đặt 2020=a; 2021=b; 2022=c, ta có :
\(\frac{bx-ay}{c}=\frac{az-cx}{b}=\frac{cy-bz}{a}\)
Theo tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{bx-ay}{c}=\frac{az-cx}{b}=\frac{cy-bz}{a}=\frac{bcx-acx}{c^2}=\frac{abz-cbx}{b^2}=\frac{acy-abz}{a^2}=\frac{bcx-acx+abz-bcx+acy-abz}{a^2+b^2+c^2}=0\)
\(\Rightarrow\hept{\begin{cases}\frac{bx-ay}{c}=0\\\frac{az-cx}{b}=0\\\frac{cy-bz}{a}=0\end{cases}}\Leftrightarrow\hept{\begin{cases}bx-ay=0\\az-cx=0\\cy-bz=0\end{cases}}\Leftrightarrow\hept{\begin{cases}ay=bx\\az=cx\\cy=bz\end{cases}}\)
Thay 2020=a; 2021=b; 2022=c, ta có :
\(\hept{\begin{cases}2020y=2021x\\2020z=2022x\\2022y=2021z\end{cases}}\Rightarrow\hept{\begin{cases}\frac{y}{2021}=\frac{x}{2020}\\\frac{z}{2022}=\frac{x}{2020}\\\frac{y}{2021}=\frac{z}{2022}\end{cases}}\)
\(\Rightarrow\frac{x}{2020}=\frac{y}{2021}=\frac{z}{2022}\)