Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Diện tích xung quanh của kho chứa:
\(S_{xq}=p\cdot d=\dfrac{12+12+12}{2}\cdot8=144\left(m^2\right)\)
Diện tích cần sơn thực tế:
\(S_s=S_{xq}-S_c=144-5=139\left(m^2\right)\)
Số tiền cần dùng để hoàn thành việc sơn là:
\(T=S_s\cdot30000=4170000\left(đ\right)\)

a) Tính được diện tích bạt phủ 2 mái lều: 20 (m2)
b) Thể tích của leeud trại là: V = 12 (m3)

Bài 6:
a: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM\(\perp\)BC
Vì M là trung điểm của BC
nên \(MB=MC=\dfrac{BC}{2}=\dfrac{12}{2}=6\left(cm\right)\)
Ta có: ΔAMB vuông tại M
=>\(AM^2+MB^2=AB^2\)
=>\(AM^2+6^2=10^2\)
=>\(AM^2+36=100\)
=>\(AM^2=100-36=64\)
=>\(AM=\sqrt{64}=8\left(cm\right)\)
b: Xét tứ giác AMCK có
I là trung điểm chung của AC và MK
=>AMCK là hình bình hành
Hình bình hành AMCK có \(\widehat{AMC}=90^0\)
nên AMCK là hình chữ nhật
c: AMCK là hình chữ nhật
=>AK//CM và AK=CM
Ta có: AK//CM
M\(\in\)BC
Do đó: AK//MB
Ta có: AK=CM
CM=MB
Do đó: AK=MB
Xét tứ giác AKMB có
AK//MB
AK=MB
Do đó: AKMB là hình bình hành
d: Để hình chữ nhật AMCK trở thành hình vuông thì AM=CM
mà \(CM=\dfrac{BC}{2}\)
nên \(AM=\dfrac{BC}{2}\)
Xét ΔABC có
AM là đường trung tuyến
\(AM=\dfrac{BC}{2}\)
Do đó: ΔABC vuông tại A
=>\(\widehat{BAC}=90^0\)
câu này đề cương trường thcs long bình dễ mà cx đi hỏi à s gà v

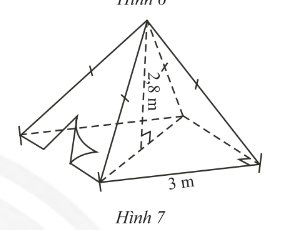
a) Thể tích không khí trong chiếc lều là: \(\frac{1}{3}{.3^2}.2,8 = 8,4\) (\({m^3}\))
b) Độ dài trung đoạn của hình chóp là: \(\sqrt {2,{8^2} + 1,{5^2}} \approx 3,18\)
Diện tích vải lều là: \(\frac{{4.3}}{2}.3,18= 19,08\) (\(c{m^2}\))

10: Chu vi đáy là 30*3=90(cm)
Diện tích xung quanh là \(90\cdot20=1800\left(cm^2\right)\)
=>Không có câu nào đúng
11;
\(V_{chóp}=\dfrac{1}{3}\cdot S_{đáy}\cdot h\)
=>\(\dfrac{1}{3}\cdot12\cdot S_{đáy}=100\)
=>\(S_{đáy}=25\left(cm^2\right)\)
Độ dài cạnh là \(\sqrt{25}=5\left(cm\right)\)
=>Chọn C

a: Chu vi đáy là 20*3=60(cm)
Diện tích xung quanh là \(17.32\cdot60=1039.2\left(cm^2\right)\)
b: Chu vi đáy là \(4\cdot3=12\left(cm\right)\)
Diện tích đáy là \(\dfrac{1}{2}\cdot3.5\cdot4=7\left(cm^2\right)\)
Diện tích xung quanh là \(12\cdot5=60\left(cm^2\right)\)
Diện tích toàn phần là \(60+7=67\left(cm^2\right)\)



Sửa đề: Độ dài cạnh đáy là 5m
Chu vi đáy là: 5+5+5=15(m)
Diện tích xung quanh là: \(\dfrac{1}{2}\cdot15\cdot5=37,5\left(m^2\right)\)
Diện tích cần sơn là: \(37,5-10=27,5\left(m^2\right)\)
Số tiền cần bỏ ra là: \(27,5\cdot120000=3300000\left(đồng\right)\)