Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 3:
Xét ΔMDC có AB//CD
nên MA/MD=MB/MC(1)
Xét ΔMDK có AI//DK
nên AI/DK=MA/MD(2)
Xét ΔMKC có IB//KC
nên IB/KC=MB/MC(3)
Từ (1), (2) và (3) suy ra AI/DK=IB/KC=MI/MK
Vì AI//KC nên AI/KC=NI/NK=NA/NC
Vì IB//DK nên IB/DK=NI/NK
=>AI/KC=IB/DK
mà AI/DK=IB/KC
nên \(\dfrac{AI}{KC}\cdot\dfrac{AI}{DK}=\dfrac{IB}{DK}\cdot\dfrac{IB}{DC}\)
=>AI=IB
=>I là trung điểm của AB
AI/DK=BI/KC
mà AI=BI
nên DK=KC
hay K là trung điểm của CD

Ta gọi E là trung điểm của DC
Vì tam giác ABC có
BM = MC
DE = EC
=> BD // ME
=> DI // ME
mà tâm giac ADE có AD = DE và DI // ME nên AI = IM (đpcm)

Câu 3:
Xét ΔMDC có AB//CD
nên MA/MD=MB/MC(1)
Xét ΔMDK có AI//DK
nên AI/DK=MA/MD(2)
Xét ΔMKC có IB//KC
nên IB/KC=MB/MC(3)
Từ (1), (2) và (3) suy ra AI/DK=IB/KC=MI/MK
Vì AI//KC nên AI/KC=NI/NK=NA/NC
Vì IB//DK nên IB/DK=NI/NK
=>AI/KC=IB/DK
mà AI/DK=IB/KC
nên \(\dfrac{AI}{KC}\cdot\dfrac{AI}{DK}=\dfrac{IB}{DK}\cdot\dfrac{IB}{DC}\)
=>AI=IB
=>I là trung điểm của AB
AI/DK=BI/KC
mà AI=BI
nên DK=KC
hay K là trung điểm của CD

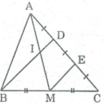
Gọi E là trung điểm của DC
Trong ΔBDC, ta có:
M là trung điểm của BC (gt)
E là trung điểm của CD (gt)
Nên ME là đường trung bình của ∆ BCD
⇒ME // BD (tính chất đường trung bình tam giác)
Suy ra: DI // ME
AD = 1/2 DC (gt)
DE = 1/2 DC (cách vẽ)
⇒ AD = DE và DI//ME
Nên AI= IM (tính chất đường trung bình của tam giác).

Gọi K là trung điểm của DC
Suy ra: AD=DK=KC
Xét ΔBDC có
M là trung điểm của BC
K là trung điểm của DC
Do đó: MK là đường trung bình của ΔBDC
Suy ra: MK//BD và \(MK=\dfrac{BD}{2}\)
hay ID//MK
Xét ΔAMK có
D là trung điểm của AK
DI//MK
Do đó: I là trung điểm của AM
hay IA=IM

Cho tam giác ABC ,điểm D thuộc cạnh AC sao cho AD = \(\frac{1}{2}\)DC .Gọi M là trung điểm của BC ,Ilaf giao điểm của AM và BD .Chứng minh rằng : IA=IM
Lấy E là trung điểm của DC
=> AD = DE = EC
Xét \(\Delta AEM\) có ME là trung bình:
=> \(ME//BD\left(ME//ID\right)\)
Xét \(\Delta AME\)có D là trung điểm của AE;ME//ID
=> I là trung điểm của AM
=>IA=IM (đpcm)
Lấy E là trung điểm của DC
\(\Rightarrow AD=DE=EC\)
Xét \(\Delta BCD\)có ME là trung bình:
\(\Rightarrow ME//BD\left(ME//ID\right)\)
Xét \(\Delta AME\)có D là trung điểm của \(AE\); \(ME//ID\)( cmt )
\(\Rightarrow I\)là trung điểm của AM
\(\Rightarrow IA=IM\left(đpcm\right)\)

Lấy N là trung điểm của DC ; ta có \(AD=DN=NC\)
Xét tam giác BCD có MN là đường trung bình \(\Rightarrow MN\text{//}BD\) hay \(MN\text{//}ID\)
Xét tam giác AMN có D là trung điểm của AN; ID//MN (cmt) => I là trung điểm của AM
=> ĐPCM

Câu 1:
* Hình thang ABCD có AB // CD
E là trung điểm của AD (gt)
F là trung điểm của BC (gt)
Nên EF là đường trung bình của hình thang ABCD
EF // CD (tỉnh chất đưòng trung bình hình thang) (1)
* Trong ΔADC ta có:
E là trung điểm của AD (gt)
I là trung điểm của AC (gt)
Nên EI là đường trung bình của ΔADC
⇒ EI // CD (tính chất đường trung bình tam giác) (2)
Từ (1) và (2) và theo tiên đề ƠClít ta có đường thẳng EF và EI trùng nhau. Vậy E, F, I thẳng hàng
Câu 2:
Gọi E là trung điểm của DC
Trong ΔBDC, ta có:
M là trung điểm của BC (gt)
E là trung điểm của CD (gt)
Nên ME là đường trung bình của ∆BCD
⇒ME // BD (tính chất đường trung bình tam giác)
Suy ra: DI // ME
AD = 1/2 DC (gt)
DE = 1/2 DC (cách vẽ)
⇒ AD = DE và DI//ME
Nên AI= IM (tính chất đường trung bình của tam giác).