Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Giải:
Ta có:
Do \(\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{1}{5}\Leftrightarrow\dfrac{1}{a}< \dfrac{1}{5}\Leftrightarrow a>5\left(1\right)\)
Ta lại có:
\(0< a< b\Leftrightarrow\dfrac{1}{a}>\dfrac{1}{b}\Leftrightarrow\dfrac{1}{a}+\dfrac{1}{a}>\dfrac{1}{a}+\dfrac{1}{b}\)
Hay \(\dfrac{2}{a}>\dfrac{1}{5}\Leftrightarrow\dfrac{2}{a}>\dfrac{2}{10}\Leftrightarrow a< 10\left(2\right)\)
Kết hợp \(\left(1\right)\) và \(\left(2\right)\Leftrightarrow a\in\left\{6;7;8;9\right\}\)
- Với \(a=6\) thì \(\dfrac{1}{b}=\dfrac{1}{5}-\dfrac{1}{6}=\dfrac{1}{30}\Leftrightarrow b=30\)
- Với \(a=7\) thì \(\dfrac{1}{b}=\dfrac{1}{5}-\dfrac{1}{7}=\dfrac{2}{35}\Leftrightarrow b=17,5\) (loại)
- Với \(a=8\) thì \(\dfrac{1}{b}=\dfrac{1}{5}-\dfrac{1}{8}=\dfrac{3}{40}\Leftrightarrow b\approx13,3\) (loại)
- Với \(a=9\) thì \(\dfrac{1}{b}=\dfrac{1}{5}-\dfrac{1}{9}=\dfrac{4}{45}\Leftrightarrow b=11,25\) (loại)
Vậy chỉ có 1 cách viết là \(\dfrac{1}{5}=\dfrac{1}{6}+\dfrac{1}{30}\)
Vì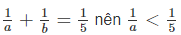 
Suy ra a > 5 (1)
Ta lại có 0 < a < b nên 
Hay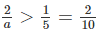 
, suy ra a < 10 (2)
Từ (1) và (2) ta có a ∈ {6;7;8;9}
Nếu a = 6 thì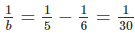 
nên b = 30
Nếu a = 7 thì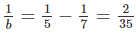 
suy ra b = 17,5 (loại)
Nếu a = 8 thì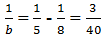 
suy ra b ≈ 13,3 (loại)
Nếu a = 9 thì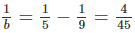 
suy ra b = 11,25 (loại)
Vậy chỉ có một cách viết là 
a) \(\dfrac{3}{8}\) và \(\dfrac{5}{27}\)
Mẫu số chung là 216
Quy đồng:
\(\dfrac{3.27}{8.27}\)=\(\dfrac{81}{216}\) ; \(\dfrac{5.8}{27.8}\)=\(\dfrac{40}{216}\)
b)\(\dfrac{-2}{9}\) và \(\dfrac{4}{25}\)
Mẫu số chung là:225
Quy đồng:
\(\dfrac{-2.25}{9.25}\)=\(\dfrac{-50}{225}\) ; \(\dfrac{4.9}{25.9}\)=\(\dfrac{36}{225}\)
c)\(\dfrac{1}{15}\) và -6
Mẫu số chung là 15
Quy đồng:
\(\dfrac{1}{15}\) ;\(\dfrac{-6.15}{15}\)=\(\dfrac{-90}{15}\)
1.
\(\dfrac{19.20}{19+20}=\dfrac{380}{39}=9\dfrac{29}{39}\)
\(\dfrac{\overline{aaa}}{\overline{aa}}=\dfrac{111.a}{11.a}=\dfrac{111}{11}=10\dfrac{1}{11}\)
\(\dfrac{\overline{ababa}}{\overline{aba}}=\dfrac{100.\overline{aba}+\overline{ba}}{\overline{aba}}=\dfrac{100.\overline{aba}}{\overline{aba}}+\dfrac{\overline{ba}}{\overline{aba}}=100\dfrac{\overline{ba}}{\overline{aba}}\)
2.
\(6\dfrac{23}{41}=\dfrac{6.41+23}{41}=\dfrac{269}{41}\)
\(a\dfrac{a}{99}=\dfrac{a.99+a}{99}=\dfrac{100.a}{99}=\dfrac{\overline{a00}}{99}\)
\(1\dfrac{a-b}{a+b}=\dfrac{a+b+a-b}{a+b}=\dfrac{2.a}{a+b}\)
3.
\(\dfrac{69}{1000}=0,069\)
\(8\dfrac{77}{100}=8,77\)
\(\dfrac{34567}{10^4}=\dfrac{34567}{10000}=3,4567\)
\(\dfrac{\overline{abc}}{10^n}=\dfrac{\overline{abc}}{10...0}=\overline{0,0...0abc}\)
n số hạng 0 n - 3 số hạng 0 ở phần thập phân
Bài 2:
a: =>11/13-5/42+x=15/18+11/13
=>x-5/42=15/18
=>x=5/6+5/42=35/42+5/42=40/42=20/21
b: 2x-3=x+1/2
=>2x-x=3+1/2
=>x=7/2
a) \(\dfrac{1}{6};\dfrac{1}{3};\dfrac{1}{2};...\)
\(\Rightarrow\dfrac{1}{6};\dfrac{2}{6};\dfrac{3}{6};...\)
Dãy có quy luật tăng dần lên 1 đơn vị ở tử số
\(\Rightarrow\) Số tiếp theo của dãy là: \(\dfrac{4}{6}\)
b) \(\dfrac{1}{8};\dfrac{5}{24};\dfrac{7}{24};...\)
\(\Rightarrow\dfrac{3}{24};\dfrac{5}{24};\dfrac{7}{24};...\)
Dãy có quy luật tăng dần lên 2 đơn vị ở tử số
\(\Rightarrow\) Số tiếp theo của dãy là: \(\dfrac{9}{24}\)
c) \(\dfrac{1}{5};\dfrac{1}{4};\dfrac{1}{3};...\)
\(\dfrac{4}{20};\dfrac{5}{20};\dfrac{6}{20};...\)
Dãy có quy luật tăng dần lên 1 đơn vị ở tử số
\(\Rightarrow\) Số tiếp theo của dãy là: \(\dfrac{7}{20}\)
d) \(\dfrac{4}{15};\dfrac{3}{10};\dfrac{1}{3};...\)
\(\Rightarrow\dfrac{8}{30};\dfrac{9}{30};\dfrac{11}{30};...\)
Dãy có quy luật tăng dần lên 1 đơn vị ở tử số
\(\Rightarrow\) Số tiếp theo của dãy là: \(\dfrac{12}{30}\)
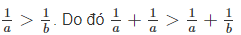
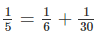
a,\(\dfrac{3}{-4}\) \(\Rightarrow\dfrac{3.\left(-1\right)}{-4.\left(-1\right)}=\dfrac{-3}{4}\)
b,\(\dfrac{-1}{-5}\)\(\Rightarrow\dfrac{-1.\left(-1\right)}{-5.\left(-1\right)}=\dfrac{1}{5}\)