K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
5 tháng 10 2018
Ta có: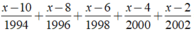
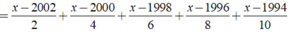
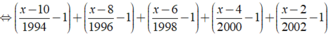
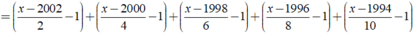
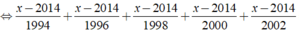
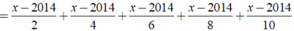
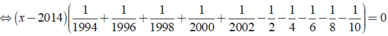
⇒ x - 2014 = 0 ⇔ x = 2014.
Vậy phương trình đã cho có nghiệm là x = 2014.
AH
Akai Haruma
Giáo viên
29 tháng 3 2020
Lời giải:
a)
$A=B\Leftrightarrow (x-3)(x+4)-2(3x-2)=(x-4)^2$
$\Leftrightarrow x^2+x-12-6x+4=x^2-8x+16$
$\Leftrightarrow 3x=24\Leftrightarrow x=8$
b)
$A=B\Leftrightarrow (x+2)(x-2)+3x^2=(2x+1)^2+2x$
$\Leftrightarrow x^2-4+3x=4x^2+6x+1$
$\Leftrightarrow 3x^2+3x+5=0$
$\Leftrightarrow 3(x+\frac{1}{2})^2=\frac{-17}{4}< 0$ (vô lý)
Do đó k có giá trị nào của $x$ để $A=B$
c)
$A=B\Leftrightarrow (x-1)(x^2+x+1)-2x=x(x-1)(x+1)$
$\Leftrightarrow x^3-1-2x=x(x^2-1)=x^3-x$
$\Leftrightarrow x=-1$
d)
$A=B\Leftrightarrow (x+1)^3-(x-2)^3=(3x-1)(3x+1)$
$\Leftrightarrow [(x+1)-(x-2)][(x+1)^2+(x+1)(x-2)+(x-2)^2]=9x^2-1$
$\Leftrightarrow 3(x^2+2x+1+x^2-x-2+x^2-4x+4)=9x^2-1$
$\Leftrightarrow 3(3x^2-3x+3)=9x^2-1$
$\Leftrightarrow -9x=-10\Leftrightarrow x=\frac{10}{9}$
V
0
BM
11 tháng 12 2017
5, a,
Ta có ƯCLN(a,b)=6 \(\Rightarrow\hept{\begin{cases}a_1.6=a\\b_1.6=b\end{cases}}\) với (a1;b1) = 1
=> a+b = a1.6+b1.6 = 6(a1+b1) = 72
=> a1+b1 = 12 = 1+11=2+10=3+9=4+8=5+7=6+6 (hoán vị của chúng)
Vì (a1,b1) = 1
=> a1+b1 = 1+11=5+7
* Với a1+b1 = 1+11
+) TH1: a1 = 1; b1=11 => a =6 và b = 66
+) TH2: a1=11; b1=1 => a=66 và b = 6
* Với a1+b1 = 5+7
+)TH1: a1=5 ; b1=7 => a=30 và b=42
+)TH2: a1=7;b1=5 => a=42 và b=30
Vậy.......
BM
11 tháng 12 2017
1, a=ƯCLN(128;48;192)
2, b= ƯCLN(300;276;252)
3, Gọi n.k+11=311 => n.k = 300
n.x + 13 = 289 => n.x = 276
=> \(n\inƯC\left(300;276\right)\)
4, G/s (2n+1;6n+5) = d (d tự nhiên)
\(\Rightarrow\hept{\begin{cases}2n+1⋮d\\6n+5⋮d\end{cases}\Rightarrow\hept{\begin{cases}3\left(2n+1\right)⋮d\\6n+5⋮d\end{cases}}}\) \(\Rightarrow\hept{\begin{cases}6n+3⋮d\\6n+5⋮d\end{cases}\Rightarrow6n+5-\left(6n+3\right)⋮d}\)
\(\Rightarrow2⋮d\Rightarrow d\in\left\{1;2\right\}\)
Vì 2n+1 lẻ => 2n+1 không chia hết cho 2
=> d khác 2 => d=1 => đpcm
3 tháng 7 2017
a,Từ x + y = 2\(\Rightarrow\)x2 + 2xy + y2 = 4
\(\Rightarrow\)2xy= 4 - (x2 + y2 ) = 4 - 10 = -6
\(\Rightarrow\)xy = -3
Ta lại có (x+y)3= x3+3x2y + 3xy2+y3
\(\Rightarrow\)x3+y3=(x+y)3-3xy(x+y)=8+9.2=26
b, Đây là cách giải tổng quát của câu a:
x3+y3=(x+y)(x2-xy+y2)=a(b-xy) (1)
Lại có: x+y=a\(\Rightarrow\)x2+2xy+y2=a2
\(\Rightarrow\)xy=\(\dfrac{a^2-\left(x^2+y^2\right)}{2}=\dfrac{a^2-b}{2}\)(2)
Từ (1) và (2) ta dễ dàng tính được:
x3+y3=\(\dfrac{a\left(3b-a^2\right)}{2}\)
Chúc các bạn học tốt
3 tháng 7 2017
a) x + y = 2 => y = 2 - x
x2 + y2 = 10
=> x2 + (2 - x)2 = 10
<=> x2 + 4 - 4x + x2 = 10
<=> 2x2 - 4x - 6 = 0
<=> x = 3 -> y = -1
hoặc x = -1 -> y = 3
TH1: x3 + y3 = 33 + (-1)3
TH2: x3 + y3 = (-1)3 + 33