

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Lời giải:
Cho hàm số y= f(x) liên tục trên [a; b] , F(x) là một nguyên hàm của f(x) trên [a; b]. Hiệu số F(b) – F(a) được gọi là tích phân từ a đến b của hàm số f(x), kí hiệu là ∫abf(x)dx.
Ta có: ∫abf(x)dx=F(x)ab=F(b)-F(a)
Ta gọi ∫ab là dấu tích phân, a là cận dưới, b là cận trên, f(x)dx biểu thức dưới dấu tích phân, f(x) là hàm số dưới dấu tích phân.
2.Các tính chất
1. ∫aaf(x)dx=0
2. ∫abf(x)dx=- ∫baf(x)dx
3. ∫bakf(x)dx=k. ∫baf(x)dx ( k là hằng số)
4. ∫ab[f(x)±g(x)]dx= ∫abf(x)dx± ∫abg(x)dx
5. ∫abf(x)dx= ∫acf(x)dx+ ∫abf(x)dx(a<c<b)

+ Phương pháp nguyên hàm từng phần:
Nếu hai hàm số u = u(x) và v = v(x) có đạo hàm liên tục trên K thì:
∫u(x).v’(x)dx = u(x).v(x) - ∫v(x).u’(x)dx
Hay viết gọn: ∫udv = uv - ∫vdv.
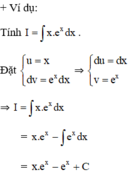

a) Đặt \(u=x^2\); \(dv=2^xdx\). Khi đó \(du=2xdx\) ; \(v=\int2^xdx=\frac{2^x}{\ln2}\) và \(I_1=x^2\frac{2^x}{\ln2}-\frac{2}{\ln2}\int x2^xdx\)
Lại áp dụng phép lấy nguyên hàm từng phần cho tích phân ở vế phải bằng cách đặt :
\(u=x\) ; \(dv=2^xdx\) và thu được \(du=dx\) ; \(v=\frac{2^x}{\ln2}\) Do đó
\(I_1=x^2\frac{2^x}{\ln_{ }2}-\frac{2}{\ln2}\left[x\frac{2^x}{\ln2}-\frac{1}{\ln2}\int2^xdx\right]\)
= \(x^2\frac{2^x}{\ln_{ }2}-\frac{2}{\ln2}\left[x\frac{2^x}{\ln2}-\frac{2^x}{\ln^22}\right]+C\) = \(\left(x^2-\frac{2}{\ln2}x+\frac{2}{\ln^22}\right)\frac{2^x}{\ln2}+C\)
b) Đặt \(u=x^2\); \(dv=e^{3x}dx\)
Khi đó \(du=2xdx\) ; \(v=\int e^{3x}dx=\frac{1}{3}\int e^{3x}d\left(3x\right)=\frac{1}{3}e^{ex}\)
Do đó:
\(I_2=\frac{x^2}{3}e^{3x}-\frac{1}{3}\int xe^{3x}dx\) (a)
Lại áp dụng phép lấy nguyên hàm từng phần cho nguyên hàm ở vế phải. Ta đặt \(u=x\) ; \(dv=e^{3x}dx\)
Khi đó \(du=dx\) ; \(v=\int e^{3x}dx=\frac{1}{3}e^{3x}\) và
\(\int xe^{ex}dx=\frac{x}{3}e^{3x}-\frac{1}{3}\int e^{3x}dx=\frac{x}{3}e^{3x}-\frac{1}{9}e^{3x}\)
Thế kết quả thu được vào (a) ta có :
\(I_2=\frac{x^2}{3}e^{3x}-\frac{2}{3}\left(\frac{x}{3}e^{3x}-\frac{1}{9}e^{3x}\right)+C=\frac{e^{3x}}{27}\left(9x^2-6x+2\right)+C\)

Cho hàm số f(x) xác định trên K.
Hàm số F(x) được gọi là nguyên hàm của hàm số f(x) trên K
⇔ F’(x) = f(x) ∀ x ∈ K.

a) Áp dụng phương pháp tìm nguyên hàm từng phần:
Đặt u= ln(1+x)
dv= xdx
=> ,
Ta có: ∫xln(1+x)dx =
=
b) Cách 1: Tìm nguyên hàm từng phần hai lần:
Đặt u= (x2+2x -1) và dv=exdx
Suy ra du = (2x+2)dx, v = ex
. Khi đó:
∫(x2+2x - 1)exdx = (x2+2x - 1)exdx - ∫(2x+2)exdx
Đặt : u=2x+2; dv=exdx
=> du = 2dx ;v=ex
Khi đó:∫(2x+2)exdx = (2x+2)ex - 2∫exdx = ex(2x+2) – 2ex+C
Vậy
∫(x2+2x+1)exdx = ex(x2-1) + C
Cách 2: HD: Ta tìm ∫(x2-1)exdx. Đặt u = x2-1 và dv=exdx.
Đáp số : ex(x2-1) + C
c) Đáp số:
HD: Đặt u=x ; dv = sin(2x+1)dx
d) Đáp số : (1-x)sinx - cosx +C.
HD: Đặt u = 1 - x ;dv = cosxdx

a) Ta có tập xác định của cả hai hàm số \(f\left(x\right),g\left(x\right)\) đểu là \(\mathbb{R}\)
Mặt khác:
\(f\left(-x\right)=\dfrac{a^{-x}+a^{-x}}{2}=f\left(x\right);g\left(x\right)=\dfrac{a^{-x}-a^x}{2}=-g\left(x\right)\)
Vậy \(f\left(x\right)\) là hàm số chẵn, \(g\left(x\right)\) làm hàm số lẻ
b) Ta có :
\(f\left(x\right)=\dfrac{a^x+a^{-x}}{2}\ge\sqrt{a^xa^{-x}}=1,\forall x\in\mathbb{R}\)
và :
\(f\left(0\right)=\dfrac{a^0+a^0}{2}=1\)
Vậy :
\(minf\left(x\right)=f\left(0\right)=1\)

Để kiểm tra một hàm F(x) có phải là một nguyên hàm của f(x) không thì ta chỉ cần kiểm tra F'(x) có bằng f(x) không?
a) \(F\left(x\right)\) là hằng số nên \(F'\left(x\right)=0\ne f\left(x\right)\)
b) \(G'\left(x\right)=2.\dfrac{1}{2}.\dfrac{1}{\cos^2x}=1+\tan^2x\)
c) \(H'\left(x\right)=\dfrac{\cos x}{1+\sin x}\)
d) \(K'\left(x\right)=-2.\dfrac{-\left(\dfrac{1}{2}.\dfrac{1}{\cos^2\dfrac{x}{2}}\right)}{\left(1+\tan\dfrac{x}{2}\right)^2}=\dfrac{\dfrac{1}{\cos^2\dfrac{x}{2}}}{\left(\dfrac{\cos\dfrac{x}{2}+\sin\dfrac{x}{2}}{\cos\dfrac{x}{2}}\right)^2}\)
\(=\dfrac{1}{\left(\cos\dfrac{x}{2}+\sin\dfrac{x}{2}\right)^2}=\dfrac{1}{1+2\cos\dfrac{x}{2}\sin\dfrac{x}{2}}\)
\(=\dfrac{1}{1+\sin x}\)
Vậy hàm số K(x) là một nguyên hàm của f(x).