NT
4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PV
1
VH
10
NA
5
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 8 2021
1.
a.
ĐKXĐ: \(x^2-1>0\Rightarrow\left[{}\begin{matrix}x>1\\x< -1\end{matrix}\right.\)
\(log_2\left(x^2-1\right)=3\)
\(\Rightarrow x^2-1=8\)
\(\Leftrightarrow x^2=9\)
\(\Rightarrow x=\pm3\) (tm)
b.
ĐKXĐ: \(x>0\)
\(log_3x+log_{\sqrt{3}}x+log_{\dfrac{1}{3}}x=6\)
\(\Leftrightarrow log_3x+2log_3x-log_3x=6\)
\(\Leftrightarrow log_3x=3\)
\(\Rightarrow x=3^3=27\)
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 8 2021
c. ĐKXĐ: \(x>0\)
\(log_{\sqrt{2}}^2x+3log_2x+log_{\dfrac{1}{2}}x=2\)
\(\Leftrightarrow\left(2log_2x\right)^2+3log_2x-log_2x=2\)
\(\Leftrightarrow4log_2^2x+2log_2x-2=0\)
\(\Rightarrow\left[{}\begin{matrix}log_2x=-1\\log_2x=\dfrac{1}{2}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\x=\sqrt{2}\end{matrix}\right.\)
CM
17 tháng 9 2017
s i n 2 x + c o s x = m <=> - c o s x 2 x + c o s x + 1 = 0
Đặt t= cos x =>
=>f’(t)=-2t + 1.
Do x ∈ [0; π] => t ∈ [-1; 1]
Số nghiệm của phương trình đã cho chính là số giao điểm của đồ thị hàm số y = f(t) và đường thẳng y = m.
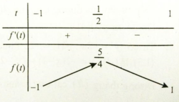
Từ bảng biến thiên ta có m ∈ (-1; 1) thì f(t)=m có 2 nghiệm
Chọn C
NM
Nguyễn Minh Quang
Giáo viên
4 tháng 10 2021
gọi n là số người trong bữa tiệc
gọi \(a_i\text{ là số cái bắt tay của người thứ i với tất các những người khác}\)
ta có \(\Sigma_{i=1}^n\text{ }a_i\text{ là một số chẵn }\)( do mỗi cái bắt tay đều được tính bởi cả hai người )
mà tổng số cái bắt tay của người bắt tay với chẵn người là số chẵn
nên tổng số cái bắt tay của người bắt tay với lẻ người cũng là số chẵn
nên phải có chẵn người trong nhóm bắt tay với lẻ người
vậy ta có điều phải chứng minh
PT
6
LT
4
KT
3
AH
Akai Haruma
Giáo viên
16 tháng 11 2017
Câu 64:
Ta có:
\(6^x+(3-m)2^x-m=0\)
\(\Leftrightarrow 6^x+3.2^x=m(1+2^x)\)
\(\Leftrightarrow \frac{6^x+3.2^x}{2^x+1}-m=0\)
Xét \(f(x)=\frac{6^x+3.2^x}{2^x+1}-m\) là một hàm liên tục. Để pt \(f(x)=0\) có nghiệm trong khoảng \((0;1)\Rightarrow f(0).f(1)< 0\)
\(\Leftrightarrow (2-m)(4-m)< 0\)
\(\Leftrightarrow 2< m< 4\Leftrightarrow m\in (2;4)\)
Đáp án C
AH
Akai Haruma
Giáo viên
16 tháng 11 2017
Câu 65:
Ta có:
\(P=\log^2_{\frac{a}{b}}a^2+3\log_b\left(\frac{a}{b}\right)\)
\(\Leftrightarrow P=[2\log_{\frac{a}{b}}a]^2+3\log_b\left(\frac{a}{b}\right)\)
\(\Leftrightarrow P=4\log^2_{\frac{a}{b}}a+3(\log_ba-\log_bb)\)
\(\Leftrightarrow P=4\log^2_{\frac{a}{b}}a+3(\log_ba-1)\)
Biến đổi: \(\log_{\frac{a}{b}}a.\log_a\left(\frac{a}{b}\right)=1\)
\(\Rightarrow \log_{\frac{a}{b}}a=\frac{1}{\log_a\left(\frac{a}{b}\right)}=\frac{1}{\log_aa-\log_ab}=\frac{1}{1-\log_ab}\)
Do đó, \(P=\frac{4}{(1-\log_ab)^2}+3(\log_ba-1)\)
Đặt \(\log_ba=x\Rightarrow \log_ab=\frac{1}{x}\)
\(P=\frac{4x^2}{(x-1)^2}+3(x-1)\). Vì \(a>b>1\Rightarrow x>1\)
\(P'=\frac{3x^3-9x^2+x-3}{(x-1)^3}=0\)
\(\Leftrightarrow 3x^3-9x^2+x-3=0\Leftrightarrow x=3\)
Lập bảng biến thiên ta suy ra \(P_{\min}=P(3)=15\)
Đáp án D
1 + 1 = 2 nha
1 + 1 = 2
Học tốt