K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
AH
Akai Haruma
Giáo viên
6 tháng 10 2018
Sửa đề : \(x^4-6x^2+8x-3=(x-1)^3(x+3)\)
Lời giải:
Ta thấy tổng các hệ số của đa thức bằng $0$ nên đa thức có nghiệm là $1$, nghĩa là khi phân tích sẽ có thừa số $x-1$ và cứ thế triển khai thôi:
\(x^4-6x^2+8x-3=(x^4-x^2)-(5x^2-5x)+(3x-3)\)
\(=x^2(x^2-1)-5x(x-1)+3(x-1)\)
\(=(x-1)[x^2(x+1)-5x+3]\)
\(=(x-1)(x^3+x^2-5x+3)\)
\(=(x-1)[x^3-x^2+2x^2-2x-(3x-3)]\)
\(=(x-1)[x^2(x-1)+2x(x-1)-3(x-1)]\)
\(=(x-1)(x^2+2x-3)(x-1)=(x-1)^2(x^2-x+3x-3)\)
\(=(x-1)^2[x(x-1)+3(x-1)]=(x-1)^2(x-1)(x+3)=(x-1)^3(x+3)\)
D
2 tháng 12 2021
*Đâu phải chia lúc nào cũng lớn hơn trừ đâu bạn,
VD: 10 : 5 = 1, Mà 10 - 5 = 5,
Vậy 10 : 5 < 10 - 5 (vì 1 < 5)
*Hay lấy ví dụ của bạn thì 10 : 9 = 1, (1) Mà 10 - 9 = 1
Vậy 10 : 9 > 10 - 9
*Cũng có trường hợp bằng nhau, ví dụ như: 4 : 2 = 2 Mà 4 - 2 = 2
Vậy 4 : 2 = 4 - 2
hoctot
.
.
.
.
CM
9 tháng 11 2017
Chọn B
Phương trình hoành độ giao điểm 
.
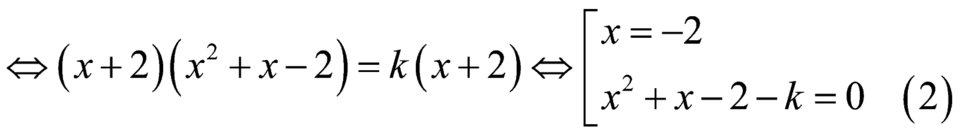Đường thẳng
cắt đồ thị hàm số 
tại 
điểm phân biệt
có hai nghiệm phân biệt khác 
Giả sử 
, 
là hai nghiệm phân biệt của 
, theo hệ thức Viet thì 
.
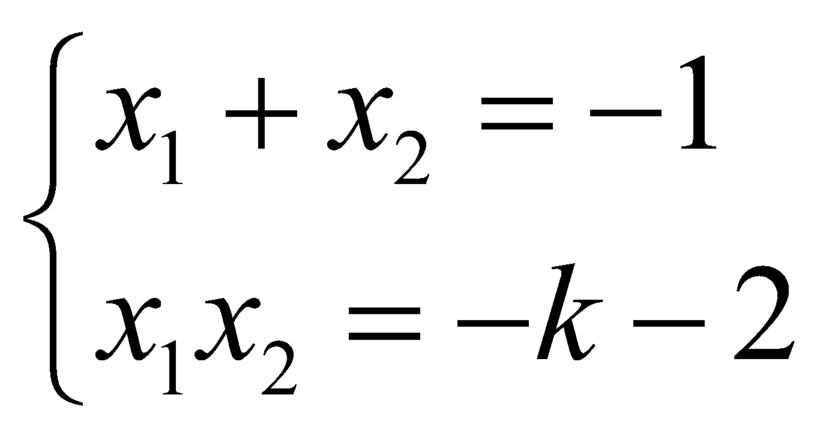Ta có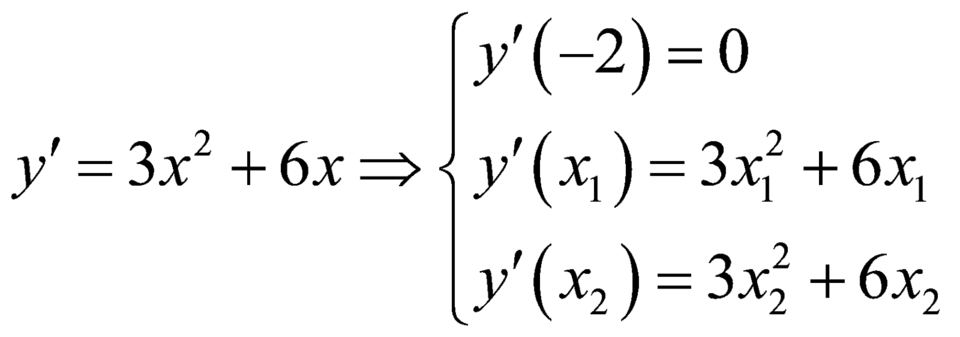 
.
Bài ra ta có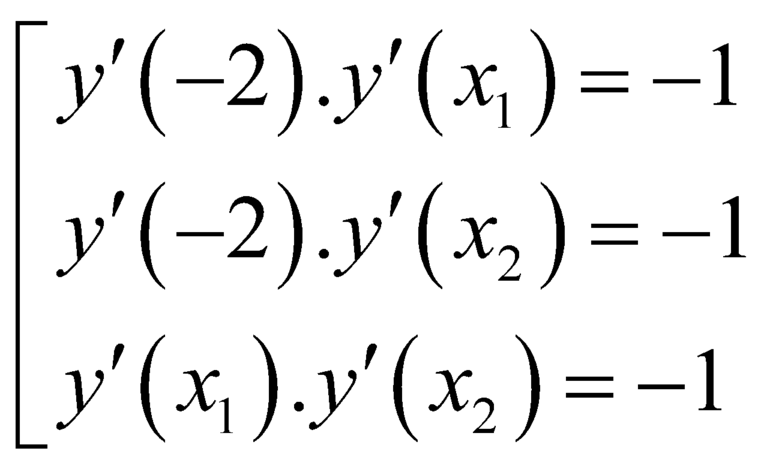 
.
Kết hợp với 
ta được 
thỏa mãn.
CM
23 tháng 10 2019
PT hoành độ giao điểm là
(3m-1) x+ 6m+ 3 == x3-3x2+ 1 hay x3-3x2 – (3m-1) x-6m-2=0 ( *)
Giả sử A( x1; y1) ; B( x2; y2) lần lượt là giao điểm của (C) và (d)
Vì B cách đều hai điểm A và C nên B là trung điểm của AC
Suy ra x1+ x3= 2x2
Thay x2= 1vào , ta có
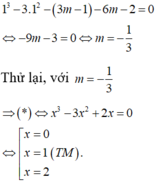
Vậy -1< m< 0
Chọn C.
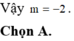
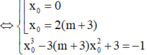
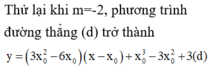
vì ba với mẹ ra con lên là 3 người nha bạn