Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

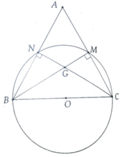
a, Ta có: B N C ^ = 90 0 => N ∈ (O; B C 2 )
B M C ^ = 90 0 => M ∈ (O; B C 2 )
=> B, C, M, N cùng thuộc đường tròn tâm (O; B C 2 )
b, ∆ABC đều có G là trực tâm đồng thời là trọng tâm
∆AOB vuông tại O có R = ON = a 2
Ta có OA = a 2 - a 2 4 = a 3 2 > R
=> A nằm ngoài (O)
Ta có OG = 1 3 OA = a 3 6 < R
=> G nằm ngoài (O)

a) AM là đường phân giác \(\widehat{BAC}\)
\(\Rightarrow\widehat{BAM}=\widehat{CAM}\)\(\Rightarrow\widebat{BM}=\widebat{CM}\)
=> M là điểm chính giữa cung BC
=> OM _|_ BC (đpcm)
b) AN là phân giác \(\widehat{CAt}\)
=> \(\widehat{tAN}=\widehat{NAC}\)mà \(\widehat{tAN}=\widehat{NCB}\)(Tứ giác ANCB nội tiếp)
và \(\widehat{NAC}=\widehat{NMC}\)(tứ gics ANCB nội tiếp)
=> \(\widehat{NCB}=\widehat{NMC}\)
Xét tam giác NCD và tam giác NMC có:
\(\widehat{MNC}\)chung
\(\widehat{NCB}=\widehat{NMC}\left(cmt\right)\)
=> Tam giác NCD đồng dạng với tam giác NMC (g.g)
=> \(\widehat{NCM}=\widehat{NDC}\)mà \(\widehat{NDC}=90^o\)và \(\widehat{NCM}=90^o\)
=> NC _|_ CM
Xét tam giác NCM nội tiếp có NC _|_ CM
=> NM là đường kính
=> N,O,M thẳng hàng
c) Tam giác MAN nội tiếp đường kín MN
=> AM _|_ AN => Tam giác KAD vuông tại A
Xét tam giác KAD vuông tại A có AI là đường trung bình
=> AI=ID
=> Tam giác AID cân tại A
=> \(\widehat{IAD}=\widehat{IDA}\)(tính chất tam giác cân) hay \(\widehat{IAB}+\widehat{BAD}=\widehat{IDA}\)
Lại có \(\widehat{DAC}+\widehat{DCA}=\widehat{IDA}\)(tính chất góc ngoài)
\(\Rightarrow\widehat{IAB}+\widehat{BAD}=\widehat{DAC}+\widehat{DCA}\)
mà \(\widehat{BAD}=\widehat{DAC}\)(AD là phân giác) => \(\widehat{IAB}=\widehat{DCA}\)
mà 2 góc này nằm ở vị trí góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung
=> IA là tiếp tuyến của (O)


( 1 số phần cơ bản sẽ làm tắt nha, cái đấy bạn sẽ tự trình bày rõ nhá, nhất là chứng minh tứ giác nội tiếp sẽ rút ngắn lại )
a)\(\widehat{ABO}=\widehat{AEO}=90^0\)
\(\Rightarrow ABEO\)nội tiếp
=> A,B,E,O thuộc 1 đường tròn
b) Xét tam giác AMC và tam giác ACN có:
\(\hept{\begin{cases}\widehat{NAC}chung\\\widehat{ACM}=\widehat{ANC}\left(=\frac{1}{2}sđ\widebat{MC}\right)\end{cases}\Rightarrow\Delta AMC~\Delta ACN\left(g-g\right)}\)
\(\Rightarrow\frac{AM}{AC}=\frac{AC}{AN}\)
\(\Rightarrow AC^2=AM.AN\)
c) \(\widehat{MJC}+\widehat{MFC}=180^0\)
\(\Rightarrow MJCF\)nội tiếp
\(\Rightarrow\widehat{MFJ}=\widehat{MCJ}\)
Mà \(\widehat{MCJ}=\widehat{MBC}\left(=\frac{1}{2}sđ\widebat{MC}\right)\)
\(\Rightarrow\widehat{MFJ}=\widehat{MBC}\left(1\right)\)
CMTT \(\widehat{MFI}=\widehat{MCB}\left(2\right)\)
Xét tam giác MBC có: \(\widehat{CMB}+\widehat{MCB}+\widehat{MBC}=180^0\left(3\right)\)
Từ (1), (2) và (3) \(\Rightarrow\widehat{CMB}+\widehat{MFJ}+\widehat{MFI}=180^0\)
\(\Rightarrow\widehat{CMB}+\widehat{PFQ}=180^0\)
\(\Rightarrow MPFQ\)nội tiếp
\(\Rightarrow\widehat{MPQ}=\widehat{MFQ}\)mà \(\widehat{MFQ}=\widehat{MBC}\left(cmt\right)\)
\(\Rightarrow\widehat{MPQ}=\widehat{MBC}\)mà 2 góc này ở vị trí đồng vị
\(\Rightarrow PQ//BC\)
d) Xét tam giác MIF và tam giác MFJ có:
\(\hept{\begin{cases}\widehat{MIF}=\widehat{MFJ}\left(=\widehat{MBF}\right)\\\widehat{MJF}=\widehat{MFI}\left(=\widehat{MCF}\right)\end{cases}\Rightarrow\Delta MIF~\Delta MFJ\left(g-g\right)}\)
\(\Rightarrow\frac{MI}{MF}=\frac{MF}{MJ}\)
\(\Rightarrow MI.MJ=MF^2\)
MI.MJ lớn nhất \(\Leftrightarrow MF^2\)lớn nhất
Mà \(MF=\frac{1}{2}MN\)
\(\Rightarrow MF^2=\frac{1}{4}MN^2\)
\(\Rightarrow MF\)lớn nhất <=> MN lớn nhất \(\Leftrightarrow MN\)là đường kính (O)
\(\Leftrightarrow M\)là điểm chính giữa cung BC
Vậy MI.MJ lớn nhất <=> M là điểm chính giữa cung BC.
( KO hiểu thì hỏi mình nha )

A C B H F G D E J
a) Do AB là tiếp tuyến của đường tròn tại B nên theo đúng định nghĩa, ta có \(OB\perp BA\Rightarrow\widehat{OBA}=90^o\)
Vậy tam giác ABO vuông tại B.
Xét tam giác vuông OAB, áp dụng định lý Pi-ta-go ta có :
\(AB=\sqrt{OA^2-OB^2}=\sqrt{4R^2-R^2}=R\sqrt{3}\)
b) Ta có BC là dây cung, \(OH\perp BC\)
Tam giác cân OBC có OH là đường cao nên nó cũng là tia phân giác góc COB.
Xét tam giác OCA và OBA có:
OC = OB ( = R)
OA chung
\(\widehat{COA}=\widehat{BOA}\) (cmt)
\(\Rightarrow\Delta OCA=\Delta OBA\left(c-g-c\right)\)
\(\Rightarrow\widehat{OCA}=\widehat{OBA}=90^o\). Vậy CA là tiếp tuyến của đường tròn (O) tại C.
c) Ta có BC là dây cung, OH vuông góc BC nên theo tính chất đường kính dây cung ta có H là trung điểm BC.
Xét tam giác vuông OBA có BH là đường cao nên áp dụng hệ thức lượng trong tam giác ta có:
\(HB.OA=OB.BA\Rightarrow HB=\frac{R.R\sqrt{3}}{2R}=\frac{R\sqrt{3}}{2}\)
Vậy thì BC = 2HB = \(R\sqrt{3}\)
Do \(\Delta OCA=\Delta OBA\Rightarrow CA=BA\)
Xét tam giác ABC có \(AB=BC=CA=R\sqrt{3}\) nên nó là tam giác đều.
d) Gọi G là trung điểm của CA; J là giao điểm của AE và HD, F' là giao điểm của AE và OB
Ta cần chứng minh F' trùng F.
Dễ thấy HD // OB; HG // AB mà \(AB\perp OB\Rightarrow HD\perp GH\) hay D là tiếp tuyến của đường tròn tại H.
Từ đó ta có : \(\widehat{EHJ}=\widehat{EAJ}\)
Vậy thì \(\Delta HEJ\sim\Delta AHJ\left(g-g\right)\Rightarrow\frac{EJ}{HJ}=\frac{HJ}{AJ}\Rightarrow HJ^2=EJ.AJ\)
Xét tam giác vuông JDA có DE là đường cao nên áp dụng hệ thức lượng trong tam giác ta có:
\(JD^2=JE.JA\)
Vậy nên HJ = JD.
Áp dụng định lý Ta let trong tam giác OAB ta có:
Do HD // OB nên \(\frac{HJ}{OF'}=\frac{JD}{F'B}\left(=\frac{AJ}{AF'}\right)\)
Mà HJ = JD nên OF' = F'B hay F' là trung điểm OB. Vậy F' trùng F.
Từ đó ta có A, E, F thẳng hàng.

a: Xét tứ giác BNMC có góc BNC=góc BMC=90 độ
nên BNMC là tứ giác nội tiếp
=>B,N,M,C cùng thuộc (O)
b: Xét (O) có
BC là đường kính
MNlà dây
Do đó: BC>MN
c: Vì ΔABC đều có G là giao của hai đường cao
nên G là tâm đường tròn ngoại tiếp ΔABC và cũng là trọng tâm
=>GA=GC và AG=2/3AO
=>GC>GO
=>G nằm trong (O)