Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
Xét hàm số f(x) = x 3 - 3 x + m .
Để GTNN của hàm số y =
x
3
-
3
x
+
m
2
trên đoạn [-1;1] bằng 1 thì ![]() hoặc
hoặc ![]()
Ta có ![]()
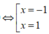
=> f(x) nghịch biến trên [-1;1]
Suy ra ![]() và
và ![]()
Trường hợp 1: ![]()
Trường hợp 2: ![]()
Vậy tổng các giá trị của tham số m là 0.

\(f'\left(x\right)=3x^2-6x=0\Rightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
\(f\left(-1\right)=-2;f\left(0\right)=2;f\left(2\right)=-2\)
\(\Rightarrow M=2;m=-2\Rightarrow P=6\)
Cả 4 đáp án đều sai (kiểm tra lại đề bài, có đúng là \(f\left(x\right)=x^3-3x^2+2\) hay không?)

Chọn B.
Ta có 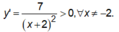
Do đó hàm số đồng biến trên [0;2].
Suy ra 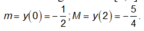
Do đó 4M – 2m = 6.

Đáp án C
Phương pháp:
- Tìm TXĐ
- Tính y’
- Lập bảng biến thiên của hàm số trên đoạn - 1 ; 1 2
- Xác định giá trị lớn nhất và giá trị nhỏ nhất của hàm số
- Tính tích M.m.
Cách giải:
TXĐ: D = R\{1}
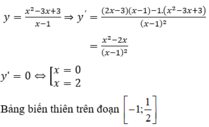
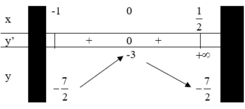
![]()
![]()

\(y'=3x^2-6x-9=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=3\end{matrix}\right.\)
a. Trên [-4;4] ta có:
\(y\left(-4\right)=-41\) ; \(y\left(-1\right)=40\) ; \(y\left(3\right)=8\) ; \(y\left(4\right)=15\)
\(\Rightarrow y_{min}=-41\) ; \(y_{max}=40\)
b. Trên [0;5] ta có:
\(y\left(0\right)=35\) ; \(y\left(3\right)=8\); \(y\left(5\right)=40\)
\(\Rightarrow y_{max}=40\) ; \(y_{min}=8\)

\(y'=6x^2+6x-12=0\Rightarrow\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.\)
\(y\left(-1\right)=14\) ; \(y\left(1\right)=-6\) ; \(y\left(5\right)=266\)
\(\Rightarrow\min\limits_{\left[-1;5\right]}y=-6\) ; \(\max\limits_{\left[-1;5\right]}y=266\)
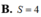

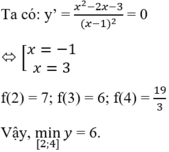
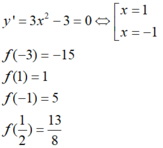
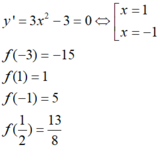
Ta có \(y'=-3<0\) nên hàm số luôn nghịch biến với mọi $x$ thuộc tập xác định.
Do đó kết hợp với \(x<2\) nên \(y>y(2)=-4\)
Dấu bằng không xảy ra cho nên hàm không có min.