Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1. Định lí Pytago
Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.
ΔABC vuông tại A thì ta có:
AB2+AC2=BC2
a2+b2=c2

a) (-\infty ; \, 2) \cap (-1; \, +\infty)(−∞;2)∩(−1;+∞)=(-1;2)
b) (−1;6) ∪ [4;8)=(-1;8]
c) (−∞;−5] ∩(−5;1)={-5}
Bài 2
a) \(x^4-24x^2-25=0\) ( 1 )
Đặt \(t=x^2\) ( điều kiện \(t\ge0\) )
\(pt\left(1\right)\Leftrightarrow t^2-24t-25=0\)
\(\Delta=b^2-4ac\)
\(\Delta=676\)
\(\Rightarrow\left\{{}\begin{matrix}t_1=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{24+\sqrt{676}}{2}=25\left(nhận\right)\\t_2=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{24-\sqrt{676}}{2}=-1\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow x^2=25\)
\(\Rightarrow x=\pm5\)
b)
\(\left\{{}\begin{matrix}2x-y=2\\9x+8y=34\end{matrix}\right.\)
Xét \(2x-y=2\)
\(\Rightarrow x=\dfrac{2+y}{2}\)
Ta có \(9x+8y=34\)
\(\Leftrightarrow\dfrac{9\left(2+y\right)}{2}+8y=34\)
\(\Leftrightarrow\dfrac{18+9y}{2}+8y=34\)
\(\Leftrightarrow\dfrac{18+25y}{2}=34\)
\(\Leftrightarrow18+25y=68\)
\(\Rightarrow y=2\)
\(\Rightarrow x=\dfrac{y+2}{2}=2\)
Vậy \(\left\{{}\begin{matrix}x=2\\y=2\end{matrix}\right.\)
Bài 3
a) \(x^2-5x+m-2=0\)
Thay \(m=-4\) vào phương trình
\(\Rightarrow x^2-5x-6=0\)
\(\Delta=b^2-4ac\)
\(\Delta=49\)
\(\Rightarrow\left\{{}\begin{matrix}x_1=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{5+\sqrt{49}}{2}=6\\x_2=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{5-\sqrt{49}}{2}=-1\end{matrix}\right.\)
b )
\(x^2-5x+m-2=0\)
\(\Delta=b^2-4ac\)
\(\Delta=33-4m\)
Theo định lý Viet
\(\Rightarrow\left\{{}\begin{matrix}P=x_1+x_2=\dfrac{-b}{a}\\S=x_1x_2=\dfrac{c}{a}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}P=x_1+x_2=5\\S=x_1x_2=m-2\end{matrix}\right.\)
Để phương trình có 2 nghiệm dương phân biệt
\(\Rightarrow\left\{{}\begin{matrix}\Delta>0\\P>0\\S>0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}33-4m>0\\m-2>0\\5>0\left(đúng\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}m< \dfrac{33}{4}\\m>2\end{matrix}\right.\)
\(\Rightarrow2< m< \dfrac{33}{4}\)
Ta có \(2\left(\dfrac{1}{\sqrt{x_1}}+\dfrac{1}{\sqrt{x_2}}\right)=3\)
\(\Leftrightarrow\dfrac{1}{\sqrt{x_1}}+\dfrac{1}{\sqrt{x_2}}=\dfrac{3}{2}\)
\(\Leftrightarrow\dfrac{\sqrt{x_1}+\sqrt{x_2}}{\sqrt{x_1x_2}}=\dfrac{3}{2}\)
\(\Leftrightarrow\left(\dfrac{\sqrt{x_1}+\sqrt{x_2}}{\sqrt{x_1x_2}}\right)^2=\dfrac{9}{4}\)
\(\Leftrightarrow\dfrac{\left(\sqrt{x_1}+\sqrt{x_2}\right)^2}{x_1x_2}=\dfrac{9}{4}\)
\(\Leftrightarrow\dfrac{x_1+x_2+2\sqrt{x_1x_2}}{x_1x_2}=\dfrac{9}{4}\)
\(\Leftrightarrow\dfrac{5+\sqrt{m-2}}{m-2}=\dfrac{9}{4}\)
\(\Leftrightarrow20+4\sqrt{m-2}=9m-18\)
\(\Leftrightarrow4\sqrt{m-2}=9m-38\)
\(\Leftrightarrow64m-128=\left(9m-38\right)^2\)
\(\Leftrightarrow64m-128=81m^2-684m+1444\)
\(\Leftrightarrow81m^2-748m+1572=0\)
\(\Delta=b^2-4ac\)
\(\Delta=50176\)
\(\Rightarrow\left\{{}\begin{matrix}m_1=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{748+\sqrt{50176}}{162}=6\\m_2=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{748-\sqrt{50176}}{162}=\dfrac{262}{81}\end{matrix}\right.\)
Vì \(2< m< \dfrac{33}{4}\)
\(\Rightarrow m\in\left\{6;\dfrac{262}{81}\right\}\)

Ta có: a2 = 25 => a = 5 độ dài trục lớn 2a = 10
b2 = 9 => b = 3 độ dài trục nhỏ 2a = 6
c2 = a2 – b2 = 25 – 9 = 16 => c = 4
Vậy hai tiêu điểm là : F1(-4 ; 0) và F2(4 ; 0)
Tọa độ các đỉnh A1(-5; 0), A2(5; 0), B1(0; -3), B2(0; 3).

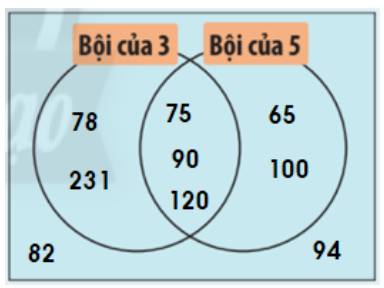
Bội của 3: 75, 78, 90, 120, 231
Bội của 5: 65, 75, 90, 100, 120
Vừa là bội của 3, vừa là bội của 5: 75, 90, 120.
Không là bội của 3 và không là bội của 5: 82, 94
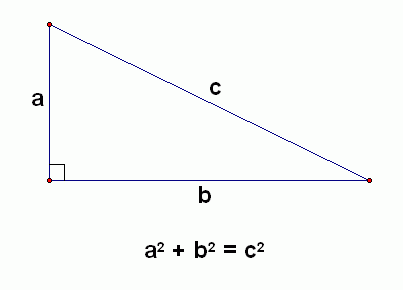

 và
và  trên hình 5 cũng có độ dài bằng nhau, nhưng liệu chúng ta có nên nói rằng chúng bằng nhau và viết
trên hình 5 cũng có độ dài bằng nhau, nhưng liệu chúng ta có nên nói rằng chúng bằng nhau và viết  thì có nhận xét gì về độ dài và hướng của chúng?
thì có nhận xét gì về độ dài và hướng của chúng?